
Given that we know the chance of getting any arbitrary number — let’s say k, because that’s a good arbitrary number — of rides in a row on Disaster Transport, using the scheme where we re-ride if the flipped coin comes up tails and stop if it comes up heads, the natural follow-up to me is: how many more rides can we expect? It’s more likely that we’d get one more ride than two, two more rides than three, three more rides than four; there’s a tiny chance we might get ten more rides; there’s a real if vanishingly tiny chance we’d get a million more rides, if Cedar Point didn’t throw us out of the park and tear the roller coaster down first.
This is another expectation value problem, the sort of thing solved with that Deal or No Deal question a few weeks back, and implicit in lottery questions and so on. The expected value of a discrete random variable — in this case, the number of rides we get — is found by taking the product of each possible outcome, such as “1”, times the probability of that outcome turning out, in this case “”, and then adding up all those products.
The probability of getting k tails in a row before the first heads was . (It’s possible we get no tails, and come up heads on the first coin flip, which is why that k+1 appears there instead of a k.) So the expected value of the number of rides is going to be:
where those trailing ellipses mean we just keep going on in the same pattern. That’s a common bit of notation, though it’s usually good form to use it only when the pattern is extremely easy to work out, such as with numbers increasing by one or two. That’s true here, but it can be that the pattern’s too elaborate to to obvious at a glance. The level of obviousness is quite variable; it’s usually about halfway between the expertise level of the instructor and that of the student. The formula can be written out explicitly making use of the capital sigma:
(If this were a mathematics textbook, the part would be underneath the Sigma, and the
part would be above it. WordPress has some ability to display mathematical expressions using LaTeX, which is very good at producing mathematics textbook formulas, but this is one it doesn’t really get quite right, at least as best as I can figure out the instructions. Please pretend that it’s printed as I wanted it to appear, because I wrote the rest of this text assuming that WordPress would do things the way I wanted, and I’ve got a cold and don’t wish to deal with modifying the text at this point.)
The formula says to evaluate the thing to the right of the sigma — — by plugging in values of k as directed under and above the sigma itself. The smallest value of k to be plugged in is 0, as at the bottom of the sigma. The second-smallest value of k to be plugged in is 0 + 1, and the third-smallest value of k is 0 + 1 + 1, and so on. The highest value of k we want to plug in is … well, infinitely large, which suggests if we want to work this out we’ll be at work a long while.
Or maybe not. I took the problem to Maple, a symbolic mathematics package able to do all sorts of algebraic and calculus manipulations that’s very much like Mathematica, because I had access to a computer which could run Maple and didn’t have one to a computer running Mathematica, a personal license for which (last time I looked) cost all the money you ever had or ever will have, plus tax. (I’m aware there’s probably an open source clone good enough for this kind of problem, but it was easier to use Maple than find it.) And that tells me this summation of infinitely many terms works out to 1.
That doesn’t mean I’m most likely to get one more ride using this scheme. As before, I have a probability of of riding the once, flipping my coin, seeing heads, and stopping. I have a probability of
of riding once, flipping the coin, getting tails, riding again, flipping the coin, getting heads, and stopping. The chance of getting two rides is a mere
. But there’s the chance of getting a large number of rides that partially overwhelms the chance of getting only the one ride.
What it means is that if you imagined everyone visiting Cedar Point — tens of thousands of people most any day — doing this same experiment, riding and flipping a coin to decide whether to re-ride — and then got from them all the count of how many times they rode, and took the arithmetic mean of all the times these thousands of people rode, you should expect that mean to be about two.
There may be something a little unsatisfying about turning to a computer to figure out this problem. I was a little unsatisfied by it. I’d like to know how it got “one”. Maybe there’s a formula I haven’t looked at which says what the sum of this particular infinitely many terms is; after all, there’s nice easy formulas for, eg, the sum of . And if there isn’t such a formula, maybe I can just take the sum of a couple of terms, the biggest and most important ones, and ignore the rest.
After all, the chance of (say) ten rides in a row is so tiny that surely I can ignore it. Even more ignorable should be the chance of eleven, or twelve, or a million, or a billion rides in a row. Nobody’s going to ride any roller coaster a billion times. (It would be a fun little side exercise, by the way, to try estimating how many times Disaster Transport — or any other roller coaster — does run, by the way, and I leave that for a future laboriously over-thought project.) Couldn’t I just ignore the probability of people getting more than ten rides, and admit that I’m making an error but it’s a small one compared to the inconvenience I’m skipping?
On the other hand, a big number times a small number can still be a moderate-sized number. Maybe the weight given to ten rides is enough to partly overcome its vanishingly small probability. (And it’s not that tiny. If twenty thousand people did this scheme, we could expect about twenty of them to get ten rides in a row from it.) And if the contribution from ten rides ins’t important, maybe the contribution of ten and eleven and twelve and so on is.
There’s still some justifying to be done to say the answer makes sense.
Is this planned to be part of a series [sic] on Zeno’s dichotomy, or are you asking your readers? because yes, there is a formula for it:
LikeLike
Uh, since I can’t post images, the general formula for geometric series is that the sum of a*r^n from n=0 to infinity is equal to a / (r – n). Wikipedia has a (somewhat informal) proof: http://en.wikipedia.org/wiki/Geometric_series#Formula
LikeLike
Ah, but this isn’t quite the geometric series. The series terms are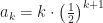 .
.
You should be able to enter LaTeX formulas by starting a block with the $ and the word ‘latex’ — no spacing between them — and ending the LaTeX block with a final $. It’s not a very robust LaTeX engine and I don’t know how to preview comments, though.
LikeLike
Oh, right, but you did mention wondering whether there was a formula for the geometric equivalent…
and yes, ‘equivalent’: it’s more than just coincidence that $\sum_{k=0}^\infty k\cdot 2^{-k-1} = \sum_{n=1}^\infty 2^{-n}$. The two sums are simply different ways of transliterating the word problem: one summing the probabilities of each complete outcome, weighted by the number of rides in each (k), and the other summing the probabilities of each individual event, weighted by the number of rides per event (1).
The formal equivalence of the general cases of both sums is a bit too much for me to attempt without neglecting my own homework, though. :P I’d still like to see what you had in store.
LikeLike
Ack, if I had read your instructions more carefully…$latex\sum_{k=0}^\infty k\cdot 2^{-k-1} = \sum_{n=1}^\infty 2^{-n}$
LikeLike
Last try: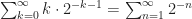
What was that were you saying about previews? :P
LikeLike
Definitely needs previews here. I may need to investigate alternate themes to find one which handles threaded comments better too, since that’s not as neatly organized as I want.
LikeLike
I’m always open to hearing what readers have to say. I have a sketch of where I mean to go with this, but would be really glad to have correspondents altering that plan.
LikeLike