Reading the Comics, April 17, 2022: Did I Catch Comic Strip Master Command By Surprise Edition

Part of the thrill of Reading the Comics posts is that the underlying material is wholly outside my control. The subjects discussed, yes, although there are some quite common themes. (Students challenging the word problem; lottery jokes; monkeys at typewriters.) But also quantity. Part of what burned me out on Reading the Comics posts back in 2020 was feeling the need to say something about lots of comic strips . Now?

I mentioned last week seeing only three interesting strips, and one of them, Andertoons, was a repeat I’d already discussed. This week there were only two strips that drew a first note and again, Andertoons was a repeat I’d already discussed. Mark Anderson’s comic for the 17th I covered in enough detail back in August of 2019. I don’t know how many new Andertoons are put into the rotation at GoComics. But the implication is Comic Strip Master Command ordered mathematics-comics production cut down, and they haven’t yet responded to my doing these again. I guess we’ll know for sure if things pick up in a couple weeks, as the lead time allows.

Rick McKee and Kent Sligh’s Mount Pleasant for the 15th of April, 2022. This is a relatively new comic strip (it only started last year), so I haven’t ever discussed it here before. Still This essay and any future ones to mention Mount Pleasant should be at this link.

So Rick McKee and Kent Sligh’s Mount Pleasant for the 15th of April is all I have to discuss. It’s part of the long series of students resisting the teacher’s question. The teacher is asking a fair enough question, that of how to do a problem that has several parts. She does ask how we “should” solve the problem of finding what 4 + 4 – 2 equals. The catch is there are several ways to do this, all of them as good. We know this if we’ve accepted subtraction as a kind of addition, and if we’ve accepted addition as commutative.

So the order is our choice. We can add 4 and 4 and then subtract 2. Or subtract 2 from the second 4, and then add that to the first 4. If you want, and can tell the difference, you could subtract 2 from the first 4, and then add the second 4 to that.

For this problem it doesn’t make any difference. But one can imagine similar ones where the order you tackle things in can make calculations easier, or harder. 5 + 7 – 2, for example, I find easier if I work it out as 5 + ( 7 – 2), that is, 5 + 5. So it’s worth taking a moment to consider whether rearranging it can make the calculation more reliable. I don’t know whether the teacher meant to challenge the students to see that there are alternatives, and no uniquely “right” answer. It’s possible McKee and Sligh did not have the teaching plan worked out.

---

That makes for another week’s worth of comic strips to discuss. All of my Reading the Comics posts should be at this link. Thanks for reading this and I will let you know if Comic Strip Master Command increases production of comics with mathematics themes.

My Little 2021 Mathematics A-to-Z: Addition

John Golden, whom so far as I know doesn’t have an active blog, suggested this week’s topic. It pairs nicely with last week’s. I link to that in text, but if you would like to read all of this year’s Little Mathematics A to Z it should be at this link. And if you’d like to see all of my A-to-Z projects, pleas try this link. Thank you.

Addition

When I wrote about multiplication I came to the peculiar conclusion that it was the same as addition. This is true only in certain lights. When we study [abstract] algebra we look at things that look like arithmetic. The simplest useful thing that looks like arithmetic is a group. It has a set of elements, and a pairwise “group operation”. That group operation we call multiplication, if we don’t have a better name. We give it two elements and it gives us one. Under certain circumstances, this multiplication looks just like addition does.

But we have reason to think addition and multiplication aren’t the same. Where do we get addition?

We can make a meaningful addition by giving it something to interact with. By adding another operation. This turns the group into a ring. As it has two operations, it’s hard to resist calling one of them addition and the other multiplication. The new multiplication follows many of the rules the addition did. Adding two elements together gives you an element in the ring. So does multiplying. Addition is associative: 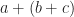is the same thing as 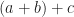. So it multiplication: is the same thing as .

And then the addition and the multiplication have to interact. If they didn’t, we’d just have a group with two operations. I don’t know anyone who’s found a good use for that. The way addition and multiplication interact we call distribution. This is represented by two rules, both of them depending on elements a, b, and c:

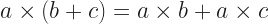
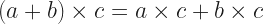
This is where we get something we have to call addition. It’s in having the two interacting group operations.

A problem which would have worried me at age eight: do we know we’re calling the correct operation “addition”? Yes, yes, names are arbitrary. But are we matching the thing we think we’re doing when we calculate 2 + 2 to addition and the thing for 2 x 2 to multiplication? How do we tell these two apart?

For all that they start the same, and resemble one another, there are differences. Addition has an identity, something that works like zero. is always , whatever is. Multiplication … the multiplication we use every day has an identity, that is, 1. Are we required to have a multiplicative identity, something so that 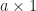is always ? That depends on what it said in the Introduction to Algebra textbook you learned on. If you want to be clear your rings do have a multiplicative identity you call it a “unit ring”. If you want to be clear you don’t care, I don’t know what to say. I’m told some people write that as “rng”, to hint that this identity is missing.

Addition always has an inverse. Whatever element you pick, there is some 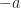so that is the additive identity. Multiplication? Even if we have a unit ring, there’s not always a reciprocal. The integers are a unit ring. But there are only two integers that have an integer multiplicative inverse, something you can multiply them by to get 1. If your unit ring does have a multiplicative inverse, this is called a division algebra. Rational numbers, for example, are a division algebra.

So for some rings, like the integers, there’s an obvious difference between addition and multiplication. But for the rational numbers? Can we tell the operations apart?

We can, through the additive identity, which please let me call 0. And the multiplicative identity, which please let me call 1. Is there a multiplicative inverse of 0? Suppose there is one; let me call it , because I need some name. Then of all the things in the world, we know this:

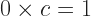
I can replace anything I like with something equal to it. So, for example, I can replace 0 with the sum of an element and its additive inverse. Like, for some element . So then:

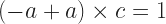
And distribute this away!

I don’t know what number 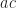is, nor what its inverse is. But I know its sum is zero. And so

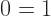
This looks like trouble. But, all right, why not have the additive and the multiplicative identities be the same number? Mathematicians like to play with all kinds of weird things; why not this weirdness?

The why not is that you work out pretty fast that every element has to be equal to every other element. If you’re not sure how, consider the starting line of that little proof, but with an element :

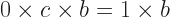
So there, finally, is a crack between addition and multiplication. Addition’s identity element, its zero, can’t have a multiplicative inverse. Multiplication’s identity element, its one, must have an additive inverse. We get addition from the thing we can’t un-multiply.

It may have struck you that if all we want is a ring with the lone element of 0 (or 1), then we can have addition and multiplication be indistinguishable again. And have the additive and multiplicative identities be the same thing. There’s nothing else for them to be. This is true, and we can. Unfortunately this ring doesn’t do much that’s interesting, except maybe prove some theorem we were working on isn’t always true. So we usually draw a box around it, acknowledge it once, and then exclude it from division algebras and fields and other things of interest. It’s much the same way we normally rule out 1 as a prime number. It’s an example that is too much bother to include given how unenlightening it is.

You can have groups and attach to them a multiplication and an addition and another binary operation. Those aren’t of such general interest that you study them much as an undergraduate.

And this is what we know of addition. It looks almost like a second multiplication. But it interacts just enough with multiplication to force the two to be distinguishable. From that we can create mathematics structures as interesting as arithmetic is.

A Summer 2015 Mathematics A To Z: ring

Ring.

Early on in her undergraduate career a mathematics major will take a class called Algebra. Actually, Introduction to Algebra is more likely, but another Algebra will follow. She will have to explain to her friends and parents that no, it’s not more of that stuff they didn’t understand in high school about expanding binomial terms and finding quadratic equations. The class is the study of constructs that work much like numbers do, but that aren’t necessarily numbers.

The first structure studied is the group. That’s made of two components. One is a set of elements. There might be infinitely many of them — the real numbers, say, or the whole numbers. Or there might be finitely many — the whole numbers from 0 up to 11, or even just the numbers 0 and 1. The other component is an operation that works like addition. What we mean by “works like addition” is that you can take two of the things in the set, “add” them together, and get something else that’s in the set. It has to be associative: something plus the sum of two other things has to equal the sum of the first two things plus the third thing. That is, 1 + (2 + 3) is the same as (1 + 2) + 3.

Also, by the rules of what makes a group, the addition has to commute. First thing plus second thing has to be the same as second thing plus first thing. That is, 1 + 2 has the same value as 2 + 1 does. Furthermore, there has to be something called the additive identity. It works like zero does in ordinary arithmetic. Anything plus the additive identity is that original thing again. And finally, everything in the group has something that’s its additive inverse. The thing plus the additive inverse is the additive identity, our zero.

If you’re lost, that’s all right. A mathematics major spends as much as four weeks in Intro to Algebra feeling lost here. But this is an example. Suppose we have a group made up of the elements 0, 1, 2, and 3. 0 will be the additive identity: 0 plus anything is that original thing. So 1 plus 0 is 1. 1 plus 1 is 2. 1 plus 2 will be 3. 1 plus 3 will be … well, make that 0 again. 2 plus 0 is 2. 2 plus 1 will be 3. 2 plus 2 will be 0. 2 plus 3 will be 1. 3 plus 0 will be 3. 3 plus 1 will be 0. 3 plus 2 will be 1. 3 plus 3 will be 2. Plus will look like a very strange word at this point.

All the elements in this have an additive inverse. Add 3 to 1 and you get 0. Add 2 to 2 and you get 0. Add 1 to 3 and you get 0. And, yes, add 0 to 0 and you get 0. This means you get to do subtraction just as well as you get to do addition.

We’re halfway there. A “ring”, introduced just as the mathematics major has got the hang of groups, is a group with a second operation. Besides being a collection of elements and an addition-like operation, a ring also has a multiplication-like operation. It doesn’t have to do much, as a multiplication. It has to be associative. That is, something times the product of two other things has to be the same as the product of the first two things times the third. You’ve seen that, though. 1 x (2 x 3) is the same as (1 x 2) x 3. And it has to distribute: something times the sum of two other things has to be the same as the sum of the something times the first thing and the something times the second. That is, 2 x (3 + 4) is the same as 2 x 3 plus 2 x 4.

For example, the group we had before, 0 times anything will be 0. 1 times anything will be what we started with: 1 times 0 is 0, 1 times 1 is 1, 1 times 2 is 2, and 1 times 3 is 3. 2 times 0 is 0, 2 times 1 is 2, 2 times 2 will be 0 again, and 2 times 3 will be 2 again. 3 times 0 is 0, 3 times 1 is 3, 3 times 2 is 2, and 3 times 3 is 1. Believe it or not, this all works out. And “times” doesn’t get to look nearly so weird as “plus” does.

And that’s all you need: a collection of things, an operation that looks a bit like addition, and an operation that looks even more vaguely like multiplication.

Now the controversy. How much does something have to look like multiplication? Some people insist that a ring has to have a multiplicative identity, something that works like 1. The ring I described has one, but one could imagine a ring that hasn’t, such as the even numbers and ordinary addition and multiplication. People who want rings to have multiplicative identity sometimes use “rng” to speak — well, write — of rings that haven’t.

Some people want rings to have multiplicative inverses. That is, anything except zero has something you can multiply it by to get 1. The little ring I built there hasn’t got one, because there’s nothing you can multiply 2 by to get 1. Some insist on multiplication commuting, that 2 times 3 equals 3 times 2.

Who’s right? It depends what you want to do. Everybody agrees that a ring has to have elements, and addition, and multiplication, and that the multiplication has to distribute across addition. The rest depends on the author, and the tradition the author works in. Mathematical constructs are things humans find interesting to study. The details of how they’re made will depend on what work we want to do.

If a mathematician wishes to make clear that she expects a ring to have multiplication that commutes and to have a multiplicative identity she can say so. She would write that something is a commutative ring with identity. Or the context may make things clear. If you’re not sure, then you can suppose she uses the definition of “ring” that was in the textbook from her Intro to Algebra class sophomore year.

It may seem strange to think that mathematicians don’t all agree on what a ring is. After all, don’t mathematicians deal in universal, eternal truths? … And they do; things that are proven by rigorous deduction are inarguably true. But the parts of these truths that are interesting are a matter of human judgement. We choose the bunches of ideas that are convenient to work with, and give names to those. That’s much of what makes this glossary an interesting project.