I’m fortunate this week to have another topic suggested again by Mr Wu, blogger and Singaporean mathematics tutor. It’s a big field, so forgive me not explaining the entire subject.
Analysis.
Analysis is about proving why the rest of mathematics works. It’s a hard field. My experience, a typical one, included crashing against real analysis as an undergraduate and again as a graduate student. It turns out mathematics works by throwing a lot of  symbols around.
symbols around.
Let me give an example. If you read pop mathematics blogs you know about the number represented by  . You’ve seen proofs, some of them even convincing, that this number equals 1. Not a tiny bit less than 1, but exactly 1. Here’s a real-analysis treatment. And — I may regret this — I recommend you don’t read it. Not closely, at least. Instead, look at its shape. Look at the words and symbols as graphic design elements, and trust that what I say is not nonsense. Resume reading after the horizontal rule.
. You’ve seen proofs, some of them even convincing, that this number equals 1. Not a tiny bit less than 1, but exactly 1. Here’s a real-analysis treatment. And — I may regret this — I recommend you don’t read it. Not closely, at least. Instead, look at its shape. Look at the words and symbols as graphic design elements, and trust that what I say is not nonsense. Resume reading after the horizontal rule.
It’s convenient to have a name for the number  . I’ll call that
. I’ll call that  , for “repeating”. 1 we’ll call 1. I think you’ll grant that whatever r is, it can’t be more than 1. I hope you’ll accept that if the difference between 1 and r is zero, then r equals 1. So what is the difference between 1 and r?
, for “repeating”. 1 we’ll call 1. I think you’ll grant that whatever r is, it can’t be more than 1. I hope you’ll accept that if the difference between 1 and r is zero, then r equals 1. So what is the difference between 1 and r?
Give me some number  . It has to be a positive number. The implication in the letter
. It has to be a positive number. The implication in the letter  is that it’s a small number. This isn’t actually required in general. We expect it. We feel surprise and offense if it’s ever not the case.
is that it’s a small number. This isn’t actually required in general. We expect it. We feel surprise and offense if it’s ever not the case.
I can show that the difference between 1 and r is less than  . I know there is some smallest counting number N so that
. I know there is some smallest counting number N so that  . For example, say
. For example, say  is 0.125. Then we can let N = 1, and
is 0.125. Then we can let N = 1, and 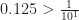 . Or suppose
. Or suppose  is 0.00625. But then if N = 3,
is 0.00625. But then if N = 3,  . (If
. (If  is bigger than 1, let N = 1.) Now we have to ask why I want this N.
is bigger than 1, let N = 1.) Now we have to ask why I want this N.
Whatever the value of r is, I know that it is more than 0.9. And that it is more than 0.99. And that it is more than 0.999. In fact, it’s more than the number you get by truncating r after any whole number N of digits. Let me call  the number you get by truncating r after N digits. So,
the number you get by truncating r after N digits. So,  and
and 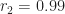 and
and  and so on.
and so on.
Since 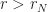 , it has to be true that
, it has to be true that  . And since we know what
. And since we know what  is, we can say exactly what
is, we can say exactly what 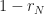 is. It's
is. It's 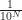 . And we picked N so that
. And we picked N so that  . So
. So 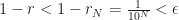 . But all we know of
. But all we know of  is that it's a positive number. It can be any positive number. So
is that it's a positive number. It can be any positive number. So 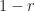 has to be smaller than each and every positive number. The biggest number that’s smaller than every positive number is zero. So the difference between 1 and r must be zero and so they must be equal.
has to be smaller than each and every positive number. The biggest number that’s smaller than every positive number is zero. So the difference between 1 and r must be zero and so they must be equal.
That is a compelling argument. Granted, it compels much the way your older brother kneeling on your chest and pressing your head into the ground compels. But this argument gives the flavor of what much of analysis is like.
For one, it is fussy, leaning to technical. You see why the subject has the reputation of driving off all but the most intent mathematics majors. If you get comfortable with this sort of argument it’s hard to notice anymore.
For another, the argument shows that the difference between two things is less than every positive number. Therefore the difference is zero and so the things are equal. This is one of mathematics’ most important tricks. And another point, there’s a lot of talk about  . And about finding differences that are, it usually turns out, smaller than some
. And about finding differences that are, it usually turns out, smaller than some  . (As an undergraduate I found something wasteful in how the differences were so often so much less than
. (As an undergraduate I found something wasteful in how the differences were so often so much less than  . We can’t exhaust the small numbers, though. It still feels uneconomic.)
. We can’t exhaust the small numbers, though. It still feels uneconomic.)
Something this misses is another trick, though. That’s adding zero. I couldn’t think of a good way to use that here. What we often get is the need to show that, say, function 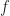 and function
and function  are equal. That is, that they are less than
are equal. That is, that they are less than  apart. What we can often do is show that
apart. What we can often do is show that 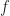 is close to some related function, which let me call
is close to some related function, which let me call  .
.
I know what you’re suspecting:  must be a polynomial. Good thought! Although in my experience, it’s actually more likely to be a piecewise constant function. That is, it’s some number, eg, “2”, for part of the domain, and then “2.5” in some other region, with no transition between them. Some other values, even values not starting with “2”, in other parts of the domain. Usually this is easier to prove stuff about than even polynomials are.
must be a polynomial. Good thought! Although in my experience, it’s actually more likely to be a piecewise constant function. That is, it’s some number, eg, “2”, for part of the domain, and then “2.5” in some other region, with no transition between them. Some other values, even values not starting with “2”, in other parts of the domain. Usually this is easier to prove stuff about than even polynomials are.
But get back to 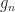 . It’s got the same deal as
. It’s got the same deal as  , some approximation easier to prove stuff about. Then we want to show that
, some approximation easier to prove stuff about. Then we want to show that  is close to some
is close to some 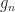 . And then show that
. And then show that  is close to
is close to 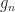 . So — watch this trick. Or, again, watch the shape of this trick. Read again after the horizontal rule.
. So — watch this trick. Or, again, watch the shape of this trick. Read again after the horizontal rule.
The difference  is equal to
is equal to  since adding zero, that is, adding the number
since adding zero, that is, adding the number 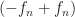 , can’t change a quantity. And
, can’t change a quantity. And  is equal to
is equal to  . Same reason:
. Same reason:  is zero. So:
is zero. So:

Now we use the “triangle inequality”. If a, b, and c are the lengths of a triangle’s sides, the sum of any two of those numbers is larger than the third. And that tells us:

And then if you can show that 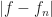 is less than
is less than  ? And that
? And that  is also
is also  ? And you see where this is going for
? And you see where this is going for 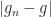 ? Then you’ve shown that
? Then you’ve shown that  . With luck, each of these little pieces is something you can prove.
. With luck, each of these little pieces is something you can prove.
Don’t worry about what all this means. It’s meant to give a flavor of what you do in an analysis course. It looks hard, but most of that is because it’s a different sort of work than you’d done before. If you hadn’t seen the adding-zero and triangle-inequality tricks? I don’t know how long you’d need to imagine them.
There are other tricks too. An old reliable one is showing that one thing is bounded by the other. That is, that  . You use this trick all the time because if you can also show that
. You use this trick all the time because if you can also show that 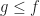 , then those two have to be equal.
, then those two have to be equal.
The good thing — and there is good — is that once you get the hang of these tricks analysis starts to come together. And even get easier. The first course you take as a mathematics major is real analysis, all about functions of real numbers. The next course in this track is complex analysis, about functions of complex-valued numbers. And it is easy. Compared to what comes before, yes. But also on its own. Every theorem in complex analysis named after Augustin-Louis Cauchy. They all show that the integral of your function, calculated along a closed loop, is zero. I exaggerate by  .
.
In grad school, if you make it, you get to functional analysis, which examines functions on functions and other abstractions like that. This, too, is easy, possibly because all the basic approaches you’ve seen several courses over. Or it feels easy after all that mucking around with the real numbers.
This is not the entirety of explaining how mathematics works. Since all these proofs depend on how numbers work, we need to show how numbers work. How logic works. But those are subjects we can leave for grad school, for someone who’s survived this gauntlet.
I hope to return in a week with a fresh A-to-Z essay. This week’s essay, and all the essays for the Little Mathematics A-to-Z, should be at this link. And all this year’s essays, and all A-to-Z essays from past years, should be at this link. Thank you once more for reading.




