Some Fun Ways to Write Numbers but Complicated

I have a delightful trifle for you today. It is, like a couple of other arithmetic games, from a paper by Inder J Taneja, who has a wonderful eye for this sort of thing. It’s based on the sort of puzzle you might use to soothe your thoughts: how can you represent a whole number, using the string of digits 1 through 9 in order, and the ordinary arithmetic operations? That is, something like 12 x 34 – 56 + 7⁸ ÷ 9? (If that would be a whole number.) Or in reverse order: 987 – 65 x 4 ÷ 3² + 1? (Again, if that’s a whole number.)

Dr Taneja has a set of answers for you, with the numbers from 0 through 11,111 written as strings of increasing and of decreasing digits. Here’s the arXiv link to the paper, for those who’d like to see the answers.

There is one missing number: Dr Taneja could find no way to produce 10,958 using the digits in increasing order. I imagine, given the paper was last updated in 2014, that there’s not a way to do this without adding some new operation such as factorials or roots, into the mix. Still, some time when you need to think of something soothing? Maybe give this a try. You might surprise everyone.

L’Hopital’s Rule Without End: Is That A Thing?

I was helping a friend learn L’Hôpital’s Rule. This is a Freshman Calculus thing. (A different one from last week, it happens. Folks are going back to school, I suppose.) The friend asked me a point I thought shouldn’t come up. I’m certain it won’t come up in the exam my friend was worried about, but I couldn’t swear it wouldn’t happen at all. So this is mostly a note to myself to think it over and figure out whether the trouble could come up. And also so this won’t be my most accessible post; I’m sorry for that, for folks who aren’t calculus-familiar.

L’Hôpital’s Rule is a way of evaluating the limit of one function divided by another, of f(x) divided by g(x). If the limit of 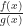has either the form of 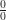or 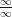then you’re not stuck. You can take the first derivative of the numerator and the denominator separately. The limit of 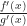if it exists will be the same value.

But it’s possible to have to do this several times over. I used the example of finding the limit, as x grows infinitely large, where f(x) = x² and g(x) = e^x. goes to 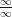as x grows infinitely large. The first derivatives, 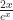, also go to 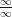. You have to repeat the process again, taking the first derivatives of numerator and denominator again. 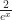finally goes to 0 as x gets infinitely large. You might have to do this a bunch of times. If f(x) were x⁷ and g(x) again e^x you’d properly need to do this seven times over. With experience you figure out you can skip some steps. Of course students don’t have the experience to know they can skip ahead to the punch line there, but that’s what the practice in homework is for.

Anyway, my friend asked whether it’s possible to get a pattern that always ends up with 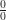or 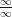and never breaks out of this. And that’s what’s got me stuck. I can think of a few patterns that would. Start out, for example, with f(x) = e^3x and g(x) = e^2x. Properly speaking, that would never end. You’d get an infinity-over-infinity pattern every derivative you took. Similarly, if you started with 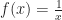and 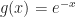you’d never come to an end. As x got infinitely large both f(x) and g(x) would go to zero and all their derivatives would be zero over and over and over and over again.

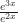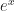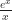But those are special cases. Anyone looking at what they were doing instead of just calculating would look at, say, and realize that’s the same as which falls out of the L’Hôpital’s Rule formulas. Or would be the same as which is an infinity-over-infinity form. But it takes only one derivative to break out of the infinity-over-infinity pattern.

So I can construct examples that never break out of a zero-over-zero or an infinity-over-infinity pattern if you calculate without thinking. And calculating without thinking is a common problem students have. Arguably it’s the biggest problem mathematics students have. But what I wonder is, are there ratios that end up in an endless zero-over-zero or infinity-over-infinity pattern even if you do think it out?

And thus this note; I’d like to nag myself into thinking about that.

How Big Is This Number?

I mentioned in a throwway bit in the article on Goldbach’s Odd Conjecture being (apparently) proven that the number had been a bound in the conjecture. That is, it was proven in 1939 that numbers larger than that had to obey the conjecture, but that it was unproven for numbers smaller than that. I described it as a number that tekes something like seven million digits to write out in full, that is, in a decimal expansion rather than some powers-of-powers sort of thing.

So let me give it a little attention as a puzzle for people who want to pass a little time doing arithmetic. Am I right to say that would be a number with about seven million digits?

The obvious way to check is to see what Google comes up with if you put 3^(3^(15)), although that turns out to be Bible quotes. Its calculator gives back Infinity, which here just means “it’s a really, really big number”. My Mac’s calculator function and my copy of Octave agree on that. It’s possible to find a better calculator that gives a meaningful answer, but you can work out roughly how big the number is just by hand, and for that matter, without resorting to anything you have to look up. I promise.

Counting To 52

fluffy brought to my attention a cute, amusing little bit from the Annals of Improbable Research, itself passing on some work by one Inder J Taneja. Taneja worked out a paper, available from arxiv.org, which lists results to the sort of mathematical puzzle that’s open to anyone with some paper and a pencil and some desire to do some recreational stuff.

Can Rex Morgan Be Made Plausible?

The comic strip Rex Morgan, MD, put up an interesting bit of nonsense in its current ridiculous story. (Rex and June are investigating a condo where nobody’s been paying rent; the residents haven’t because everyone living there is strippers who’re raising money for a cancer-stricken compatriot; the details are dopier, and much more slowly told, than this makes it sound.) But on the 7th this month it put up one of those things that caught me. Never mind the claim that Delores here (the cancer-stricken woman) puts up about being able to sense pregnancy. She claims she can predict the sex of the unborn child with 97 percent accuracy.

Is that plausible? Well, she may be just making the number up, since putting a decimal or a percentage into a number carries connotations of “only a fool would dare question me” similar to those of holding a clipboard and glaring at it while walking purposefully around. If she’s doing ordinary human-style rounding off, that could mean that she’s guessed five of six pregnancies correctly. I could believe a person thinking that makes her 97 percent accurate, but I wouldn’t be convinced by the claim and I doubt you would either.

So here’s a little recreational puzzle for you: how many pregnancies would Delores have to have predicted, and how many called accurately, for the claim of 97 percent accuracy to be hard to dismiss? How many until it isn’t clearly just luck or a small sample size?

Trivial Little Baseball Puzzle

I’ve been reading a book about the innovations of baseball so that’s probably why it’s on my mind. And this isn’t important and I don’t expect it to go anywhere, but it did cross my mind, so, why not give it 200 words where they won’t do any harm?

Imagine one half-inning in a baseball game; imagine that there’s no substitutions or injuries or anything requiring the replacement of a batter. Also suppose there are none of those freak events like when a batter hits out of order and the other team doesn’t notice (or pretends not to notice), the sort of things which launch one into the wonderful and strange world of stuff baseball does because they did it that way in 1835 when everyone playing was striving to be a Gentleman.

What’s the maximum number of runs that could be scored while still having at least one player not get a run?

My Problem With 7

My reposted problem of a couple days ago, about building all the digits of a clock face using exactly three 9’s and simple arithmetic combinations of them, caught in my mind, as these things will sometimes do. The original page missed out on a couple ways of using exactly three 9’s to make a 1, but it’s easy to do. The first thing to wonder about was how big a number could we make using exactly three 9’s? There must be some limit; it’d be absurd to think that we could make absolutely any positive integer with so primitive a tool set — surely 19,686 is out of the realm of attainability — but where is it?

Reblog: Ummm… What time is it?

Math 4 Most put up a lovely little challenge here, to find a typo in a novelty clock face. As usual for this sort of novelty clock face the various expressions come out to the familiar old 1, 2, 3, et cetera up through 12; so, can you spot one (or more than one) that doesn’t come out right?

Every couple years someone in my family buys me one of the mathematical-puzzle calendars, where there’s a bit of arithmetic to work out for each day. (For example, something for today might ask the square root of 196, although dressed up to be more interesting.) It’s good mental practice working through it, the equivalent of doing the daily Jumble word puzzle or a Sudoku problem. I admit I’m more inclined to the Jumble since I like many of the wrong words that come up in trying to unscramble ‘Object’ and ‘Recipe’. (Those are the words causing more more trouble than any in the common Jumble vocabulary.)

Math 4 Most

Can you find the typo?!

As I troll through the web, I often wander through sites that have some pretty humorous math related content.  When I find some I’d like to share, I’ll add them to this page.  I will try to keep whatever I post to the PG level at most.  (Yes there is risqué math, who knew!?)

NOTE: I do not own nor imply ownership of any images I find on the web.  Whenever possible, I will provide info on the rightful owner.  If you discover a picture/link which I have incorrectly attributed, please let me know!

This picture has been going around Facebook for a while… but it has a typo!! Do you see it?

View original post

What I Call Some Impossible Logic Problems

I’m sorry to go another day without following up the essay I meant to follow up, but it’s been a frantically busy week on a frantically busy month and something has to give somewhere. But before I return the Symbolic Logic book to the library — Project Gutenberg has the first part of it, but the second is soundly in copyright, I would expect (its first publication in a recognizable form was in the 1970s) — I wanted to pick some more stuff out of the second part.

How Many Trapezoids Can You Draw?

All the popular mathematics blogs seem to challenge readers to come up with answers; I might as well try the same, so I can be disheartened by the responses. In a pair of earlier essays I talked about the problem of drawing differently-shaped trapezoids so as to not overlook figures that might be trapezoids just because the intuition focuses on one shape over others.

So how many different shapes of trapezoids are there to draw? Let me lay out some ground rules.