In Our Time podcast repeats episode on Zeno’s Paradoxes

It seems like barely yesterday I was giving people a tip about this podcast. In Our Time, a BBC panel-discussion programme about topics of general interest, this week repeated an episode about Zeno’s Paradoxes. It originally ran in 2016.

The panel this time is two philosophers and a mathematician, which is probably about the correct blend to get the topic down. The mathematician here is Marcus du Sautoy, with the University of Oxford, who’s a renowned mathematics popularizer in his own right. That said I think he falls into a trap that we STEM types often have in talking about Zeno, that of thinking the problem is merely “how can we talk about an infinity of something”. Or “how can we talk about an infinitesimal of something”. Mathematicians have got what seem to be a pretty good hold on how to do these calculations. But that we can provide a logically coherent way to talk about, say, how a line can be composed of points with no length does not tell us where the length of a line comes from. Still, du Sautoy knows rather a few things that I don’t. (The philosophers are Barbara Sattler, with the University of St Andrews, and James Warren, with the University of Cambridge. I know nothing further of either of them.)

The episode also discusses the Quantum Zeno Effect. This is physics, not mathematics, but it’s unsettling nonetheless. The time-evolution of certain systems can be stopped, or accelerated, by frequent measurements of the system. This is not something Zeno would have been pondering. But it is a challenge to our intuition about how change ought to work.

I’ve written some of my own thoughts about some of Zeno’s paradoxes, as well as on the Sorites paradox, which is discussed along the way in this episode. And the episode has prompted new thoughts in me, particularly about what it might mean to do infinitely many things. And what a “thing” might be. This is probably a topic Zeno was hoping listeners would ponder.

How Differential Calculus Works

I’m at a point in my Why Stuff Can Orbit essays where I need to talk about derivatives. If I don’t then I’m going to be stuck with qualitative talk that’s too hard to focus on anything. But it’s a big subject. It’s about two-fifths of a Freshman Calculus course and one of the two main legs of calculus. So I want to pull out a quick essay explaining the important stuff.

Derivatives, also called differentials, are about how things change. By “things” I mean “functions”. And particularly I mean functions which have as a domain that’s in the real numbers and a range that’s in the real numbers. That’s the starting point. We can define derivatives for functions with domains or ranges that are vectors of real numbers, or that are complex-valued numbers, or are even more exotic kinds of numbers. But those ideas are all built on the derivatives for real-valued functions. So if you get really good at them, everything else is easy.

Derivatives are the part of calculus where we study how functions change. They’re blessed with some easy-to-visualize interpretations. Suppose you have a function that describes where something is at a given time. Then its derivative with respect to time is the thing’s velocity. You can build a pretty good intuitive feeling for derivatives that way. I won’t stop you from it.

A function’s derivative is itself a function. The derivative doesn’t have to be constant, although it’s possible. Sometimes the derivative is positive. This means the original function increases as whatever its variable is increases. Sometimes the derivative is negative. This means the original function decreases as its variable increases. If the derivative is a big number this means it’s increasing or decreasing fast. If the derivative is a small number it’s increasing or decreasing slowly. If the derivative is zero then the function isn’t increasing or decreasing, at least not at this particular value of the variable. This might be a local maximum, where the function’s got a larger value than it has anywhere else nearby. It might be a local minimum, where the function’s got a smaller value than it has anywhere else nearby. Or it might just be a little pause in the growth or shrinkage of the function. No telling, at least not just from knowing the derivative is zero.

Derivatives tell you something about where the function is going. We can, and in practice often do, make approximations to a function that are built on derivatives. Many interesting functions are real pains to calculate. Derivatives let us make polynomials that are as good an approximation as we need and that a computer can do for us instead.

Derivatives can change rapidly. That’s all right. They’re functions in their own right. Sometimes they change more rapidly and more extremely than the original function did. Sometimes they don’t. Depends what the original function was like.

Not every function has a derivative. Functions that have derivatives don’t necessarily have them at every point. A function has to be continuous to have a derivative. A function that jumps all over the place doesn’t really have a direction, not that differential calculus will let us suss out. But being continuous isn’t enough. The function also has to be … well, we call it “differentiable”. The word at least tells us what the property is good for, even if it doesn’t say how to tell if a function is differentiable. The function has to not have any corners, points where the direction suddenly and unpredictably changes.

Otherwise differentiable functions can have some corners, some non-differentiable points. For instance the height of a bouncing ball, over time, looks like a bunch of upside-down U-like shapes that suddenly rebound off the floor and go up again. Those points interrupting the upside-down U’s aren’t differentiable, even though the rest of the curve is.

It’s possible to make functions that are nothing but corners and that aren’t differentiable anywhere. These are done mostly to win quarrels with 19th century mathematicians about the nature of the real numbers. We use them in Real Analysis to blow students’ minds, and occasionally after that to give a fanciful idea a hard test. In doing real-world physics we usually don’t have to think about them.

So why do we do them? Because they tell us how functions change. They can tell us where functions momentarily don’t change, which are usually important. And equations with differentials in them, known in the trade as “differential equations”. They’re also known to mathematics majors as “diffy Q’s”, a name which delights everyone. Diffy Q’s let us describe physical systems where there’s any kind of feedback. If something interacts with its surroundings, that interaction’s probably described by differential equations.

So how do we do them? We start with a function that we’ll call ‘f’ because we’re not wasting more of our lives figuring out names for functions and we’re feeling smugly confident Turkish authorities aren’t interested in us.

Turkey bans books that include random F and G letters in math problems — initials of Fethullah Gulen. https://t.co/S7YwxYLxDH

— Mahir Zeynalov (@MahirZeynalov) October 6, 2016

f’s domain is real numbers, for example, the one we’ll call ‘x’. Its range is also real numbers. f(x) is some number in that range. It’s the one that the function f matches with the domain’s value of x. We read f(x) aloud as “the value of f evaluated at the number x”, if we’re pretending or trying to scare Freshman Calculus classes. Really we say “f of x” or maybe “f at x”.

There’s a couple ways to write down the derivative of f. First, for example, we say “the derivative of f with respect to x”. By that we mean how does the value of f(x) change if there’s a small change in x. That difference matters if we have a function that depends on more than one variable, if we had an “f(x, y)”. Having several variables for f changes stuff. Mostly it makes the work longer but not harder. We don’t need that here.

But there’s a couple ways to write this derivative. The best one if it’s a function of one variable is to put a little ‘ mark: f'(x). We pronounce that “f-prime of x”. That’s good enough if there’s only the one variable to worry about. We have other symbols. One we use a lot in doing stuff with differentials looks for all the world like a fraction. We spend a lot of time in differential calculus explaining why it isn’t a fraction, and then in integral calculus we do some shady stuff that treats it like it is. But that’s $\frac{df}{dx}$ . This also appears as $\frac{d}{dx} f$ . If you encounter this do not cross out the d’s from the numerator and denominator. In this context the d’s are not numbers. They’re actually operators, which is what we call a function whose domain is functions. They’re notational quirks is all. Accept them and move on.

How do we calculate it? In Freshman Calculus we introduce it with this expression involving limits and fractions and delta-symbols (the Greek letter that looks like a triangle). We do that to scare off students who aren’t taking this stuff seriously. Also we use that formal proper definition to prove some simple rules work. Then we use those simple rules. Here’s some of them.

The derivative of something that doesn’t change is 0.
The derivative of xⁿ, where n is any constant real number — positive, negative, whole, a fraction, rational, irrational, whatever — is n x^n-1.
If f and g are both functions and have derivatives, then the derivative of the function f plus g is the derivative of f plus the derivative of g. This probably has some proper name but it’s used so much it kind of turns invisible. I dunno. I’d call it something about linearity because “linearity” is what happens when adding stuff works like adding numbers does.
If f and g are both functions and have derivatives, then the derivative of the function f times g is the derivative of f times the original g plus the original f times the derivative of g. This is called the Product Rule.
If f and g are both functions and have derivatives we might do something called composing them. That is, for a given x we find the value of g(x), and then we put that value in to f. That we write as f(g(x)). For example, “the sine of the square of x”. Well, the derivative of that with respect to x is the derivative of f evaluated at g(x) times the derivative of g. That is, f'(g(x)) times g'(x). This is called the Chain Rule and believe it or not this turns up all the time.
If f is a function and C is some constant number, then the derivative of C times f(x) is just C times the derivative of f(x), that is, C times f'(x). You don’t really need this as a separate rule. If you know the Product Rule and that first one about the derivatives of things that don’t change then this follows. But who wants to go through that many steps for a measly little result like this?
Calculus textbooks say there’s this Quotient Rule for when you divide f by g but you know what? The one time you’re going to need it it’s easier to work out by the Product Rule and the Chain Rule and your life is too short for the Quotient Rule. Srsly.
There’s some functions with special rules for the derivative. You can work them out from the Real And Proper Definition. Or you can work them out from infinitely-long polynomial approximations that somehow make sense in context. But what you really do is just remember the ones anyone actually uses. The derivative of e^x is e^x and we love it for that. That’s why e is that 2.71828(etc) number and not something else. The derivative of the natural log of x is 1/x. That’s what makes it natural. The derivative of the sine of x is the cosine of x. That’s if x is measured in radians, which it always is in calculus, because it makes that work. The derivative of the cosine of x is minus the sine of x. Again, radians. The derivative of the tangent of x is um the square of the secant of x? I dunno, look that sucker up. The derivative of the arctangent of x is $\frac{1}{1 + x^2}$ and you know what? The calculus book lists this in a table in the inside covers. Just use that. Arctangent. Sheesh. We just made up the “secant” and the “cosecant” to haze Freshman Calculus students anyway. We don’t get a lot of fun. Let us have this. Or we’ll make you hear of the inverse hyperbolic cosecant.

So. What’s this all mean for central force problems? Well, here’s what the effective potential energy V(r) usually looks like:

$V_{eff}(r) = C r^n + \frac{L^2}{2 m r^2}$

So, first thing. The variable here is ‘r’. The variable name doesn’t matter. It’s just whatever name is convenient and reminds us somehow why we’re talking about this number. We adapt our rules about derivatives with respect to ‘x’ to this new name by striking out ‘x’ wherever it appeared and writing in ‘r’ instead.

Second thing. C is a constant. So is n. So is L and so is m. 2 is also a constant, which you never think about until a mathematician brings it up. That second term is a little complicated in form. But what it means is “a constant, which happens to be the number $\frac{L^2}{2m}$ , multiplied by r^-2”.

So the derivative of V_eff, with respect to r, is the derivative of the first term plus the derivative of the second. The derivatives of each of those terms is going to be some constant time r to another number. And that’s going to be:

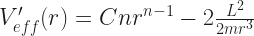
$V'_{eff}(r) = C n r^{n - 1} - 2 \frac{L^2}{2 m r^3}$

And there you can divide the 2 in the numerator and the 2 in the denominator. So we could make this look a little simpler yet, but don’t worry about that.

OK. So that’s what you need to know about differential calculus to understand orbital mechanics. Not everything. Just what we need for the next bit.

Spontaneity and the performance of work

I’d wanted just to point folks to the latest essay in the CarnotCycle blog. This thermodynamics piece is a bit about how work gets done, and how it relates to two kinds of variables describing systems. The two kinds are known as intensive and extensive variables, and considering them helps guide us to a different way to regard physical problems.

carnotcycle

Imagine a perfect gas contained by a rigid-walled cylinder equipped with a frictionless piston held in position by a removable external agency such as a magnet. There are finite differences in the pressure (P1>P2) and volume (V2>V1) of the gas in the two compartments, while the temperature can be regarded as constant.

If the constraint on the piston is removed, will the piston move? And if so, in which direction?

Common sense, otherwise known as dimensional analysis, tells us that differences in volume (dimensions L³) cannot give rise to a force. But differences in pressure (dimensions ML^-1T^-2) certainly can. There will be a net force of P1–P2 per unit area of piston, driving it to the right.

– – – –

The driving force

In thermodynamics, there exists a set of variables which act as “generalised forces” driving a system from one state to…

View original post 290 more words

Reading the Comics, September 8, 2014: What Is The Problem Edition

Must be the start of school or something. In today’s roundup of mathematically-themed comics there are a couple of strips that I think touch on the question of defining just what the problem is: what are you trying to measure, what are you trying to calculate, what are the rules of this sort of calculation? That’s a lot of what’s really interesting about mathematics, which is how I’m able to say something about a rerun Archie comic. It’s not easy work but that’s why I get that big math-blogger paycheck.

Edison Lee works out the shape of the universe, and as ever in this sort of thing, he forgot to carry a number. — I’d have thought the universe to be at least three-dimensional.

John Hambrock’s The Brilliant Mind of Edison Lee (September 2) talks about the shape of the universe. Measuring the world, or the universe, is certainly one of the older influences on mathematical thought. From a handful of observations and some careful reasoning, for example, one can understand how large the Earth is, and how far away the Moon and the Sun must be, without going past the kinds of reasoning or calculations that a middle school student would probably be able to follow.

There is something deeper to consider about the shape of space, though: the geometry of the universe affects what things can happen in them, and can even be seen in the kinds of physics that happen. A famous, and astounding, result by the mathematical physicist Emmy Noether shows that symmetries in space correspond to conservation laws. That the universe is, apparently, rotationally symmetric — everything would look the same if the whole universe were picked up and rotated (say) 80 degrees along one axis — means that there is such a thing as the conservation of angular momentum. That the universe is time-symmetric — the universe would look the same if it had got started five hours later (please pretend that’s a statement that can have any coherent meaning) — means that energy is conserved. And so on. It may seem, superficially, like a cosmologist is engaged in some almost ancient-Greek-style abstract reasoning to wonder what shapes the universe could have and what it does, but (putting aside that it gets hard to divide mathematics, physics, and philosophy in this kind of field) we can imagine observable, testable consequences of the answer.

Zach Weinersmith’s Saturday Morning Breakfast Cereal (September 5) tells a joke starting with “two perfectly rational perfectly informed individuals walk into a bar”, along the way to a joke about economists. The idea of “perfectly rational perfectly informed” people is part of the mathematical modeling that’s become a popular strain of economic thought in recent decades. It’s a model, and like many models, is properly speaking wrong, but it allows one to describe interesting behavior — in this case, how people will make decisions — without complications you either can’t handle or aren’t interested in. The joke goes on to the idea that one can assign costs and benefits to continuing in the joke. The idea that one can quantify preferences and pleasures and happiness I think of as being made concrete by Jeremy Bentham and the utilitarian philosophers, although trying to find ways to measure things has been a streak in Western thought for close to a thousand years now, and rather fruitfully so. But I wouldn’t have much to do with protagonists who can’t stay around through the whole joke either.

Marc Anderson’s Andertoons (September 6) was probably composed in the spirit of joking, but it does hit something that I understand baffles kids learning it every year: that subtracting a negative number does the same thing as adding a positive number. To be fair to kids who need a couple months to feel quite confident in what they’re doing, mathematicians needed a couple generations to get the hang of it too. We have now a pretty sound set of rules for how to work with negative numbers, that’s nice and logically tested and very successful at representing things we want to know, but there seems to be a strong intuition that says “subtracting a negative three” and “adding a positive three” might just be different somehow, and we won’t really know negative numbers until that sense of something being awry is resolved.

Andertoons pops up again the next day (September 7) with a completely different drawing of a chalkboard and this time a scientist and a rabbit standing in front of it. The rabbit’s shown to be able to do more than multiply and, indeed, the mathematics is correct. Cosines and sines have a rather famous link to exponentiation and to imaginary- and complex-valued numbers, and it can be useful to change an ordinary cosine or sine into this exponentiation of a complex-valued number. Why? Mostly, because exponentiation tends to be pretty nice, analytically: you can multiply and divide terms pretty easily, you can take derivatives and integrals almost effortlessly, and then if you need a cosine or a sine you can get that out at the end again. It’s a good trick to know how to do.

Jeff Harris’s Shortcuts children’s activity panel (September 9) is a page of stuff about “Geometry”, and it’s got some nice facts (some mathematical, some historical), and a fair bunch of puzzles about the field.

Morrie Turner’s Wee Pals (September 7, perhaps a rerun; Turner died several months ago, though I don’t know how far ahead of publication he was working) features a word problem in terms of jellybeans that underlines the danger of unwarranted assumptions in this sort of problem-phrasing.

Moose has trouble working out 15 percent of $8.95; Jughead explains why. — How far back is this rerun from if Moose got lunch for two for $8.95?

Craig Boldman and Henry Scarpelli’s Archie (September 8, rerun) goes back to one of arithmetic’s traditional comic strip applications, that of working out the tip. Poor Moose is driving himself crazy trying to work out 15 percent of $8.95, probably from a quiz-inspired fear that if he doesn’t get it correct to the penny he’s completely wrong. Being able to do a calculation precisely is useful, certainly, but he’s forgetting that in tis real-world application he gets some flexibility in what has to be calculated. He’d save some effort if he realized the tip for $8.95 is probably close enough to the tip for $9.00 that he could afford the difference, most obviously, and (if his budget allows) that he could just as well work out one-sixth the bill instead of fifteen percent, and give up that workload in exchange for sixteen cents.

Mark Parisi’s Off The Mark (September 8) is another entry into the world of anthropomorphized numbers, so you can probably imagine just what π has to say here.

Reading the Comics, August 29, 2014: Recurring Jokes Edition

Well, I did say we were getting to the end of summer. It’s taken only a couple days to get a fresh batch of enough mathematics-themed comics to include here, although the majority of them are about mathematics in ways that we’ve seen before, sometimes many times. I suppose that’s fair; it’s hard to keep thinking of wholly original mathematics jokes, after all. When you’ve had one killer gag about “537”, it’s tough to move on to “539” and have it still feel fresh.

Tom Toles’s Randolph Itch, 2 am (August 27, rerun) presents Randolph suffering the nightmare of contracting a case of entropy. Entropy might be the 19th-century mathematical concept that’s most achieved popular recognition: everyone knows it as some kind of measure of how disorganized things are, and that it’s going to ever increase, and if pressed there’s maybe something about milk being stirred into coffee that’s linked with it. The mathematical definition of entropy is tied to the probability one will find whatever one is looking at in a given state. Work out the probability of finding a system in a particular state — having particles in these positions, with these speeds, maybe these bits of magnetism, whatever — and multiply that by the logarithm of that probability. Work out that product for all the possible ways the system could possibly be configured, however likely or however improbable, just so long as they’re not impossible states. Then add together all those products over all possible states. (This is when you become grateful for learning calculus, since that makes it imaginable to do all these multiplications and additions.) That’s the entropy of the system. And it applies to things with stunning universality: it can be meaningfully measured for the stirring of milk into coffee, to heat flowing through an engine, to a body falling apart, to messages sent over the Internet, all the way to the outcomes of sports brackets. It isn’t just body parts falling off.

Stanley's old algebra teacher insists there is yet hope for him. — Randy Glasbergen’s _The Better Half_ For the 28th of August, 2014.

Randy Glasbergen’s The Better Half (August 28) does the old joke about not giving up on algebra someday being useful. Do teachers in other subjects get this? “Don’t worry, someday your knowledge of the Panic of 1819 will be useful to you!” “Never fear, someday they’ll all look up to you for being able to diagram a sentence!” “Keep the faith: you will eventually need to tell someone who only speaks French that the notebook of your uncle is on the table of your aunt!”

Eric the Circle (August 28, by “Gilly” this time) sneaks into my pages again by bringing a famous mathematical symbol into things. I’d like to make a mention of the links between mathematics and music which go back at minimum as far as the Ancient Greeks and the observation that a lyre string twice as long produced the same note one octave lower, but lyres and strings don’t fit the reference Gilly was going for here. Too bad.

Zach Weinersmith’s Saturday Morning Breakfast Cereal (August 28) is another strip to use a “blackboard full of mathematical symbols” as visual shorthand for “is incredibly smart stuff going on”. The symbols look to me like they at least started out as being meaningful — they’re the kinds of symbols I expect in describing the curvature of space, and which you can find by opening up a book about general relativity — though I’m not sure they actually stay sensible. (It’s not the kind of mathematics I’ve really studied.) However, work in progress tends to be sloppy, the rough sketch of an idea which can hopefully be made sound.

Anthony Blades’s Bewley (August 29) has the characters stare into space pondering the notion that in the vastness of infinity there could be another of them out there. This is basically the same existentially troublesome question of the recurrence of the universe in enough time, something not actually prohibited by the second law of thermodynamics and the way entropy tends to increase with the passing of time, but we have already talked about that.

Reading the Comics, July 24, 2014: Math Is Just Hard Stuff, Right? Edition

Maybe there is no pattern to how Comic Strip Master Command directs the making of mathematics-themed comic strips. It hasn’t quite been a week since I had enough to gather up again. But it’s clearly the summertime anyway; the most common theme this time seems to be just that mathematics is some hard stuff, without digging much into particular subjects. I can work with that.

Pab Sungenis’s The New Adventures of Queen Victoria (July 19) brings in Erwin Schrödinger and his in-strip cat Barfly for a knock-knock joke about proof, with Andrew Wiles’s name dropped probably because he’s the only person who’s gotten to be famous for a mathematical proof. Wiles certainly deserves fame for proving Fermat’s Last Theorem and opening up what I understand to be a useful new field for mathematical research (Fermat’s Last Theorem by itself is nice but unimportant; the tools developed to prove it, though, that’s worthwhile), but remembering only Wiles does slight Richard Taylor, whose help Wiles needed to close a flaw in his proof.

Incidentally I don’t know why the cat is named Barfly. It has the feel to me of a name that was a punchline for one strip and then Sungenis felt stuck with it. As Thomas Dye of the web comic Newshounds said, “Joke names’ll kill you”. (I’m inclined to think that funny names can work, as the Marx Brotehrs, Fred Allen, and Vic and Sade did well with them, but they have to be a less demanding kind of funny.)

What I would change about my comic: I would never've named a character "General Swallowemup." Joke names'll kill you (see Funky Winkerbean).

— Thomas K. Dye (@newshoundscomic) July 19, 2014

John Deering’s Strange Brew (July 19) uses a panel full of mathematical symbols scrawled out as the representation of “this is something really hard being worked out”. I suppose this one could also be filed under “rocket science themed comics”, but it comes from almost the first problem of mathematical physics: if you shoot something straight up, how long will it take to fall back down? The faster the thing starts up, the longer it takes to fall back, until at some speed — the escape velocity — it never comes back. This is because the size of the gravitational attraction between two things decreases as they get farther apart. At or above the escape velocity, the thing has enough speed that all the pulling of gravity, from the planet or moon or whatever you’re escaping from, will not suffice to slow the thing down to a stop and make it fall back down.

The escape velocity depends on the size of the planet or moon or sun or galaxy or whatever you’re escaping from, of course, and how close to the surface (or center) you start from. It also assumes you’re talking about the speed when the thing starts flying away, that is, that the thing doesn’t fire rockets or get a speed boost by flying past another planet or anything like that. And things don’t have to reach the escape velocity to be useful. Nothing that’s in earth orbit has reached the earth’s escape velocity, for example. I suppose that last case is akin to how you can still get some stuff done without getting out of the recliner.

Mel Henze’s Gentle Creatures (July 21) uses mathematics as the standard for proving intelligence exists. I’ve got a vested interest in supporting that proposition, but I can’t bring myself to say more than that it shows a particular kind of intelligence exists. I appreciate the equation of the final panel, though, as it can be pretty well generalized.

To disguise a sports venue it's labelled ``Math Arena'', with ``lectures on the actual odds of beating the casino''. — Bill Holbrook’s _Safe Havens_ for the 22nd of July, 2014.

Bill Holbrook’s Safe Havens (July 22) plays on mathematics’ reputation of being not very much a crowd-pleasing activity. That’s all right, although I think Holbrook makes a mistake by having the arena claim to offer a “lecture on the actual odds of beating the casino”, since the mathematics of gambling is just the sort of mathematics I think would draw a crowd. Probability enjoys a particular sweet spot for popular treatment: many problems don’t require great amounts of background to understand, and have results that are surprising, but which have reasons that are easy to follow and don’t require sophisticated arguments, and are about problems that are easy to imagine or easy to find interesting: cards being drawn, dice being rolled, coincidences being found, or secrets being revealed. I understand Holbrook’s editorial cartoon-type point behind the lecture notice he put up, but the venue would have better scared off audiences if it offered a lecture on, say, “Chromatic polynomials for rigidly achiral graphs: new work on Yamada’s invariant”. I’m not sure I could even explain that title in 1200 words.

Missy Meyer’s Holiday Doodles (July 22) revelas to me that apparently the 22nd of July was “Casual Pi Day”. Yeah, I suppose that passes. I didn’t see much about it in my Twitter feed, but maybe I need some more acquaintances who don’t write dates American-fashion.

Thom Bluemel’s Birdbrains (July 24) again uses mathematics — particularly, Calculus — as not just the marker for intelligence but also as The Thing which will decide whether a kid goes on to success in life. I think the dolphin (I guess it’s a dolphin?) parent is being particularly horrible here, as it’s not as if a “B+” is in any way a grade to be ashamed of, and telling kids it is either drives them to give up on caring about grades, or makes them send whiny e-mails to their instructors about how they need this grade and don’t understand why they can’t just do some make-up work for it. Anyway, it makes the kid miserable, it makes the kid’s teachers or professors miserable, and for crying out loud, it’s a B+.

(I’m also not sure whether a dolphin would consider a career at Sea World success in life, but that’s a separate and very sad issue.)

Reading the Comics, June 4, 2014: Intro Algebra Edition

I’m not sure that there is a theme to the most recent mathematically-themed comic strips that I’ve seen, all from GoComics in the past week, but they put me in mind of the stuff encountered in learning algebra, so let’s run with that. It’s either that or I start making these “edition” titles into something absolutely and utterly meaningless, which could be.

Marc Anderson’s Andertoons (May 30) uses the classic setup of a board full of equation to indicate some serious, advanced thinking going on, and then puts in a cute animal twist on things. I don’t believe that the equation signifies anything, but I have to admit I’m not sure. It looks quite plausibly like something which might turn up in quantum mechanics (the “h” and “c” and lambda are awfully suggestive), so if Anderson made it up out of whole cloth he did an admirable job. If he didn’t make it up and someone recognizes it, please, let me know; I’m curious what it might be.

Marc Anderson reappears on the second of June has the classic reluctant student upset with the teacher who knew all along what x was. Knowledge of what x is is probably the source of most jokes about learning algebra, or maybe mathematics overall, and it’s amusing to me anyway that what we really care about is not what x is particularly — we don’t even do ourselves any harm if we call it some other letter, or for that matter an empty box — but learning how to figure out what values in the place of x would make the relationship true.

Jonathan Lemon’s Rabbits Against Magic (May 31) has the one-eyed rabbit Weenus doing miscellaneous arithmetic on the way to punning about things working out. I suppose to get to that punch line you have to either have mathematics or gym class as the topic, and I wouldn’t be surprised if Lemon’s done a version with those weight-lifting machines on screen. That’s not because I doubt his creativity, just that it’s the logical setup.

Eric Scott’s Back In The Day (June 2) has a pair of dinosaurs wondering about how many stars there are. Astronomy has always inspired mathematics. After one counts the number of stars one gets to wondering, how big the universe could be — Archimedes, classically, estimated the universe was about big enough to hold 10⁶³ grains of sand — or how far away the sun might be — which the Ancient Greeks were able to estimate to the right order of magnitude on geometric grounds — and I imagine that looking deep into the sky can inspire the idea that the infinitely large and the infinitely small are at least things we can try to understand. Trying to count stars is a good start.

Steve Boreman’s Little Dog Lost (June 2) has a stick insect provide the excuse for some geometry puns.

Brian and Ron Boychuk’s The Chuckle Brothers (June 4) has a pie shop gag that I bet the Boychuks are kicking themselves for not having published back in mid-March.

The ideal gas equation

I did want to mention that the CarnotCycle big entry for the month is “The Ideal Gas Equation”. The Ideal Gas equation is one of the more famous equations that isn’t F = ma or E = mc², which I admit is’t a group of really famous equations; but, at the very least, its content is familiar enough.

If you keep a gas at constant temperature, and increase the pressure on it, its volume decreases, and vice-versa, known as Boyle’s Law. If you keep a gas at constant volume, and decrease its pressure, its temperature decreases, and vice-versa, known as Gay-Lussac’s law. Then Charles’s Law says if a gas is kept at constant pressure, and the temperature increases, then the volume increases, and vice-versa. (Each of these is probably named for the wrong person, because they always are.) The Ideal Gas equation combines all these relationships into one, neat, easily understood package.

Peter Mander describes some of the history of these concepts and equations, and how they came together, with the interesting way that they connect to the absolute temperature scale, and of absolute zero. Absolute temperatures — Kelvin — and absolute zero are familiar enough ideas these days that it’s difficult to remember they were ever new and controversial and intellectually challenging ideas to develop. I hope you enjoy.

carnotcycle

If you received formal tuition in physical chemistry at school, then it’s likely that among the first things you learned were the 17th/18th century gas laws of Mariotte and Gay-Lussac (Boyle and Charles in the English-speaking world) and the equation that expresses them: PV = kT.

It may be that the historical aspects of what is now known as the ideal (perfect) gas equation were not covered as part of your science education, in which case you may be surprised to learn that it took 174 years to advance from the pressure-volume law PV = k to the combined gas law PV = kT.

The lengthy timescale indicates that putting together closely associated observations wasn’t regarded as a must-do in this particular era of scientific enquiry. The French physicist and mining engineer Émile Clapeyron eventually created the combined gas equation, not for its own sake, but because he needed an…

View original post 1,628 more words

Underground Maps, And Making Your Own

By way of the UK Ed Chat web site I’ve found something that’s maybe useful in mathematical education and yet just irresistible to my sort of mind. It’s the Metro Map Creator, a tool for creating maps in the style and format of those topographical, circuit-diagram-style maps made famous by the London Underground and many subway or rail systems with complex networks to describe.

UK Ed Chat is of the opinion it can be used to organize concepts by how they lead to one another and how they connect to other concepts. I can’t dispute that, but what tickles me is that it’s just so beautiful to create maps like this. There’s a reason I need to ration the time I spend playing Sid Meier’s Railroads.

It also brings to mind that in the early 90s I attended a talk by someone who was in the business of programming automated mapmaking software. If you accept that it’s simple to draw a map, as in a set of lines describing a location, at whatever scale and over whatever range is necessary, there’s still an important chore that’s less obviously simple: how do you label it? Labels for the things in the map have to be close to — but not directly on — the thing being labelled, but they also have to be positioned so as not to overlap other labels that have to be there, and also to not overlap other important features, although they might be allowed to run over something unimportant. Add some other constraints, such as the label being allowed to rotate a modest bit but not too much (we can’t really have a city name be upside-down), and working out a rule by which to set a label’s location becomes a neat puzzle.

As I remember from that far back, the solution (used then) was to model each label’s position as if it were an object on the end of a spring which had some resting length that wasn’t zero — so that the label naturally moves away from the exact position of the thing being labelled — but with a high amount of friction — as if the labels were being dragged through jelly — with some repulsive force given off by the things labels must not overlap, and simulate shaking the entire map until it pretty well settles down. (In retrospect I suspect the lecturer was trying to talk about Monte Carlo simulations without getting into too much detail about that, when the simulated physics of the labels were the point of the lecture.)

This always struck me as a neat solution as it introduced a bit of physics into a problem which hasn’t got any on the assumption that a stable solution to the imposed physical problem will turn out to be visually appealing. It feels like an almost comic reversal of the normal way that mathematics and physics interact.

Pardon me, now, though, as I have to go design many, many imaginary subway systems.

Reading the Comics, April 21, 2014: Bill Amend In Name Only Edition

Recently the National Council of Teachers of Mathematics met in New Orleans. Among the panelists was Bill Amend, the cartoonist for FoxTrot, who gave a talk about the writing of mathematics comic strips. Among the items he pointed out as challenges for mathematics comics — and partly applicable to any kind of teaching of mathematics — were:

Accessibility
Stereotypes
What is “easy” and “hard”?
I’m not exactly getting smarter as I age
Newspaper editors might not like them

Besides the talk (and I haven’t found a copy of the PowerPoint slides of his whole talk) he also offered a collection of FoxTrot comics with mathematical themes, good for download and use (with credit given) for people who need to stock up on them. The link might be expire at any point, note, so if you want them, go now.

While that makes a fine lead-in to a collection of mathematics-themed comic strips around here I have to admit the ones I’ve seen the last couple weeks haven’t been particularly inspiring, and none of them are by Bill Amend. They’ve covered a fair slate of the things you can write mathematics comics about — physics, astronomy, word problems, insult humor — but there’s still interesting things to talk about. For example:

Continue reading “Reading the Comics, April 21, 2014: Bill Amend In Name Only Edition”

How Dirac Made Every Number

A couple weeks back I offered a challenge taken from Graham Farmelo’s biography (The Strangest Man) of the physicist Paul Dirac. The physicist had been invited into a game to create whole numbers by using exactly four 2’s and the normal arithmetic operations, for example:

$1 = \frac{2 + 2}{2 + 2}$

$2 = 2^{2 - \left(2 \div 2\right)}$

$4 = 2^2 \div 2 + 2$

$8 = 2^{2^{2}} \div 2$

While four 2’s have to be used, and not any other numerals, it’s permitted to use the 2’s stupidly, as every one of my examples here does. Dirac went off and worked out a scheme for producing any positive integer from them. Now, if all goes well, Dirac’s answer should be behind this cut and it hasn’t been spoiled in the reader or the mails sent out to people reading it.

The answer made me slap my forehead and cry “of course”, if that helps you work it out before you look.

Weightlessness at the Equator (Whiteboard Sketch #1)

The mathematics blog Scientific Finger Food has an interesting entry, “Weightlessness at the Equator (Whiteboard Sketch #1)”, which looks at the sort of question that’s easy to imagine when you’re young: since gravity pulls you to the center of the earth, and the earth’s spinning pushes you away (unless we’re speaking precisely, but you know what that means), so, how fast would the planet have to spin so that a person on the equator wouldn’t feel any weight?

It’s a straightforward problem, one a high school student ought to be able to do. Sebastian Templ works the problem out, though, including the all-important diagram that shows the important part, which is what calculation to do.

In reality, the answer doesn’t much matter since a planet spinning nearly fast enough to allow for weightlessness at the equator would be spinning so fast it couldn’t hold itself together, and a more advanced version of this problem could make use of that: given some measure of how strongly rock will hold itself together, what’s the fastest that the planet can spin before it falls apart? And a yet more advanced course might work out how other phenomena, such as tides or the precession of the poles might work. Eventually, one might go on to compose highly-regarded works of hard science fiction, if you’re willing to start from the questions easy to imagine when you’re young.

scientific finger food

At the present time, our Earth does a full rotation every 24 hours, which results in day and night. Just like on a carrousel, its inhabitants (and, by the way, all the other stuff on and of the planet) are pushed “outwards” due to the centrifugal force. So we permanently feel an “upwards” pulling force thanks to the Earth’s rotation. However, the centrifugal force is much weaker than the centri petal force, which is directed towards the core of the planet and usually called “gravitation”. If this wasn’t the case, we would have serious problems holding our bodies down to the ground. (The ground, too, would have troubles holding itself “to the ground”.)

Especially on the equator, the centrifugal and the gravitational force are antagonistic forces: the one points “downwards” while the other points “upwards”.

How fast would the Earth have to spin in order to cause weightlessness at the…

View original post 201 more words

Can You Be As Clever As Dirac For A Little Bit

I’ve been reading Graham Farmelo’s The Strangest Man: The Hidden Life of Paul Dirac, which is a quite good biography about a really interestingly odd man and important physicist. Among the things mentioned is that at one point Dirac was invited in to one of those number-challenge puzzles that even today sometimes make the rounds of the Internet. This one is to construct whole numbers using exactly four 2’s and the normal, non-exotic operations — addition, subtraction, exponentials, roots, the sort of thing you can learn without having to study calculus. For example:

$1 = \left(2 \div 2\right) \cdot \left(2 \div 2\right)$
$2 = 2 \cdot 2^{\left(2 - 2\right)}$
$3 = 2 + \left(\frac{2}{2}\right)^2$
$4 = 2 + 2 + 2 - 2$

Now these aren’t unique; for example, you could also form 2 by writing $2 \div 2 + 2 \div 2$ , or as $2^{\left(2 + 2\right)\div 2}$ . But the game is to form as many whole numbers as you can, and to find the highest number you can.

Dirac went to work and, complained his friends, broke the game because he found a formula that can any positive whole number, using exactly four 2’s.

I couldn’t think of it, and had to look to the endnotes to find what it was, but you might be smarter than me, and might have fun playing around with it before giving up and looking in the endnotes yourself. The important things are, it has to produce any positive integer, it has to use exactly four 2’s (although they may be used stupidly, as in the examples I gave above), and it has to use only common arithmetic operators (an ambiguous term, I admit, but, if you can find it on a non-scientific calculator or in a high school algebra textbook outside the chapter warming you up to calculus you’re probably fine). Good luck.

The Liquefaction of Gases – Part II

The CarnotCycle blog has a continuation of last month’s The Liquefaction of Gases, as you might expect, named The Liquefaction of Gases, Part II, and it’s another intriguing piece. The story here is about how the theory of cooling, and of phase changes — under what conditions gases will turn into liquids — was developed. There’s a fair bit of mathematics involved, although most of the important work is in in polynomials. If you remember in algebra (or in pre-algebra) drawing curves for functions that had x³ in them, and in finding how they sometimes had one and sometimes had three real roots, then you’re well on your way to understanding the work which earned Johannes van der Waals the 1910 Nobel Prize in Physics.

carnotcycle

Future Nobel Prize winners both. Kamerlingh Onnes and Johannes van der Waals in 1908.

On Friday 10 July 1908, at Leiden in the Netherlands, Kamerlingh Onnes succeeded in liquefying the one remaining gas previously thought to be non-condensable – helium – using a sequential Joule-Thomson cooling technique to drive the temperature down to just 4 degrees above absolute zero. The event brought to a conclusion the race to liquefy the so-called permanent gases, following the revelation that all gases have a critical temperature below which they must be cooled before liquefaction is possible.

This crucial fact was established by Dr. Thomas Andrews, professor of chemistry at Queen’s College Belfast, in his groundbreaking study of the liquefaction of carbon dioxide, “On the Continuity of the Gaseous and Liquid States of Matter”, published in the Philosophical Transactions of the Royal Society of London in 1869.

As described in Part I of…

View original post 2,047 more words

Reading the Comics, February 21, 2014: Circumferences and Monkeys Edition

And now to finish off the bundle of mathematic comics that I had run out of time for last time around. Once again the infinite monkeys situation comes into play; there’s also more talk about circumferences than average.

Brian and Ron Boychuk’s The Chuckle Brothers (February 13) does a little wordplay on how “circumference” sounds like it could kind of be a knightly name, which I remember seeing in a minor Bugs Bunny cartoon back in the day. “Circumference” the word derives from the Latin, “circum” meaning around and “fero” meaning “to carry”; and to my mind, the really interesting question is why do we have the words “perimeter” and “circumference” when it seems like either one would do? “Circumference” does have the connotation of referring to just the boundary of a circular or roughly circular form, but why should the perimeter of circular things be so exceptional as to usefully have its own distinct term? But English is just like that, I suppose.

Paul Trapp’s Thatababy (February 13) brings back the infinite-monkey metaphor. The infinite monkeys also appear in John Deering’s Strange Brew (February 20), which is probably just a coincidence based on how successfully tossing in lots of monkeys can produce giggling. Or maybe the last time Comic Strip Master Command issued its orders it sent out a directive, “more infinite monkey comics!”

Ruben Bolling’s Tom The Dancing Bug (February 14) delivers some satirical jabs about Biblical textual inerrancy by pointing out where the Bible makes mathematical errors. I tend to think nitpicking the Bible mostly a waste of good time on everyone’s part, although the handful of arithmetic errors are a fair wedge against the idea that the text can’t have any errors and requires no interpretation or even forgiveness, with the Ezra case the stronger one. The 1 Kings one is about the circumference and the diameter for a vessel being given, and those being incompatible, but it isn’t hard to come up with a rationalization that brings them plausibly in line (you have to suppose that the diameter goes from outer wall to outer wall, while the circumference is that of an inner wall, which may be a bit odd but isn’t actually ruled out by the text), which is why I think it’s the weaker.

Bill Whitehead’s Free Range (February 16) uses a blackboard full of mathematics as a generic “this is something really complicated” signifier. The symbols as written don’t make a lot of sense, although I admit it’s common enough while working out a difficult problem to work out weird bundles of partly-written expressions or abuses of notation (like on the middle left of the board, where a bracket around several equations is shown as being less than a bracket around fewer equations), just because ideas are exploding faster than they can be written out sensibly. Hopefully once the point is proven you’re able to go back and rebuild it all in a form which makes sense, either by going into standard notation or by discovering that you have soem new kind of notation that has to be used. It’s very exciting to come up with some new bit of notation, even if it’s only you and a couple people you work with who ever use it. Developing a good way of writing a concept might be the biggest thrill in mathematics, even better than proving something obscure or surprising.

Jonathan Lemon’s Rabbits Against Magic (February 18) uses a blackboard full of mathematics symbols again to give the impression of someone working on something really hard. The first two lines of equations on 8-Ball’s board are the time-dependent Schrödinger Equations, describing how the probability distribution for something evolves in time. The last line is Euler’s formula, the curious and fascinating relationship between pi, the base of the natural logarithm e, imaginary numbers, one, and zero.

Todd Clark’s Lola (February 20) uses the person-on-an-airplane setup for a word problem, in this case, about armrest squabbling. Interesting to me about this is that the commenters get into a squabble about how airplane speeds aren’t measured in miles per hour but rather in nautical miles, although nobody not involved in air traffic control really sees that. What amuses me about this is that what units you use to measure the speed of the plane don’t matter; the kind of work you’d do for a plane-travelling-at-speed problem is exactly the same whatever the units are. For that matter, none of the unique properties of the airplane, such as that it’s travelling through the air rather than on a highway or a train track, matter at all to the problem. The plane could be swapped out and replaced with any other method of travel without affecting the work — except that airplanes are more likely than trains (let’s say) to have an armrest shortage and so the mock question about armrest fights is one in which it matters that it’s on an airplane.

Bill Watterson’s Calvin and Hobbes (February 21) is one of the all-time classics, with Calvin wondering about just how fast his sledding is going, and being interested right up to the point that Hobbes identifies mathematics as the way to know. There’s a lot of mathematics to be seen in finding how fast they’re going downhill. Measuring the size of the hill and how long it takes to go downhill provides the average speed, certainly. Working out how far one drops, as opposed to how far one travels, is a trigonometry problem. Trying the run multiple times, and seeing how the speed varies, introduces statistics. Trying to answer questions like when are they travelling fastest — at a single instant, rather than over the whole run — introduce differential calculus. Integral calculus could be found from trying to tell what the exact distance travelled is. Working out what the shortest or the fastest possible trips introduce the calculus of variations, which leads in remarkably quick steps to optics, statistical mechanics, and even quantum mechanics. It’s pretty heady stuff, but I admit, yeah, it’s math.

The Liquefaction of Gases – Part I

I know, or at least I’m fairly confident, there’s a couple readers here who like deeper mathematical subjects. It’s fine to come up with simulated Price is Right games or figure out what grades one needs to pass the course, but those aren’t particularly challenging subjects.

But those are hard to write, so, while I stall, let me point you to CarnotCycle, which has a nice historical article about the problem of liquefaction of gases, a problem that’s not just steeped in thermodynamics but in engineering. If you’re a little familiar with thermodynamics you likely won’t be surprised to see names like William Thomson, James Joule, or Willard Gibbs turn up. I was surprised to see in the additional reading T O’Conor Sloane show up; science fiction fans might vaguely remember that name, as he was the editor of Amazing Stories for most of the 1930s, in between Hugo Gernsback and Raymond Palmer. It’s often a surprising world.

carnotcycle

On Monday 3 December 1877, the French Academy of Sciences received a letter from Louis Cailletet, a 45 year-old physicist from Châtillon-sur-Seine. The letter stated that Cailletet had succeeded in liquefying both carbon monoxide and oxygen.

Liquefaction as such was nothing new to 19th century science, it should be said. The real news value of Cailletet’s announcement was that he had liquefied two gases previously considered ‘non condensable’.

While a number of gases such as chlorine, carbon dioxide, sulfur dioxide, hydrogen sulfide, ethylene and ammonia had been liquefied by the simultaneous application of pressure and cooling, the principal gases comprising air – nitrogen and oxygen – together with carbon monoxide, nitric oxide, hydrogen and helium, had stubbornly refused to liquefy, despite the use of pressures up to 3000 atmospheres. By the mid-1800s, the general opinion was that these gases could not be converted into liquids under any circumstances.

But in…

View original post 1,334 more words

CarnotCycle on the Gibbs-Helmholtz Equation

I’m a touch late discussing this and can only plead that it has been December after all. Over on the CarnotCycle blog — which is focused on thermodynamics in a way I rather admire — was recently a discussion of the Gibbs-Helmholtz Equation, which turns up in thermodynamics classes, and goes a bit better than the class I remember by showing a couple examples of actually using it to understand how chemistry works. Well, it’s so easy in a class like this to get busy working with symbols and forget that thermodynamics is a supremely practical science [1].

The Gibbs-Helmholtz Equation — named for Josiah Willard Gibbs and for Hermann von Helmholtz, both of whom developed it independently (Helmholtz first) — comes in a couple of different forms, which CarnotCycle describes. All these different forms are meant to describe whether a particular change in a system is likely to happen. CarnotCycle’s discussion gives a couple of examples of actually working out the numbers, including for the Haber process, which I don’t remember reading about in calculative detail before. So I wanted to recommend it as a bit of practical mathematics or physics.

[1] I think it was Stephen Brush pointed out many of the earliest papers in thermodynamics appeared in railroad industry journals, because the problems of efficiently getting power from engines, and of how materials change when they get below freezing, are critically important to turning railroads from experimental contraptions into a productive industry. The observation might not be original to him. The observation also might have been Wolfgang Schivelbusch’s instead.

What’s The Point Of Hamiltonian Mechanics?

The Diff_Eq twitter feed had a link the other day to a fine question put on StackExchange.com: What’s the Point of Hamiltonian Mechanics? Hamiltonian Mechanics is a different way of expressing the laws of Newtonian mechanics from what you learn in high school, and what you learn from that F equals m a business, and it gets introduced in the Mechanics course you take early on as a physics major.

At this level of physics you’re mostly concerned with, well, the motion of falling balls, of masses hung on springs, of pendulums swinging back and forth, of satellites orbiting planets. This is all nice tangible stuff and you can work problems out pretty well if you know all the forces the moving things exert on one another, forming a lot of equations that tell you how the particles are accelerating, from which you can get how the velocities are changing, from which you can get how the positions are changing.

The Hamiltonian formation starts out looking like it’s making life harder, because instead of looking just at the positions of particles, it looks at both the positions and the momentums (which is the product of the mass and the velocity). However, instead of looking at the forces, particularly, you look at the energy in the system, which typically is going to be the kinetic energy plus the potential energy. The energy is a nice thing to look at, because it’s got some obvious physical meaning, and you should know how it changes over time, and because it’s just a number (a scalar, in the trade) instead of a vector, the way forces are.

And here’s a neat thing: the way the position changes over time is found by looking at how the energy would change if you made a little change in the momentum; and the way the momentum changes over time is found by looking at how the energy would change if you made a little change in the position. As that sentence suggests, that’s awfully pretty; there’s something aesthetically compelling about treating position and momentum so very similarly. (They’re not treated in exactly the same way, but it’s close enough.) And writing the mechanics problem this way, as position and momentum changing in time, means we can use tools that come from linear algebra and the study of matrices to answer big questions like whether the way the system moves is stable, which are hard to answer otherwise.

The questioner who started the StackExchange discussion pointed out that before they get to Hamiltonian mechanics, the course also introduced the Euler-Lagrange formation, which looks a lot like the Hamiltonian, and which was developed first, and gets introduced to students first; why not use that? Here I have to side with most of the commenters about the Hamiltonian turning out to be more useful when you go on to more advanced physics. The Euler-Lagrange form is neat, and particularly liberating because you get an incredible freedom in how you set up the coordinates describing the action of your system. But it doesn’t have that same symmetry in treating the position and momentum, and you don’t get the energy of the system built right into the equations you’re writing, and you can’t use the linear algebra and matrix tools that were introduced. Mostly, the good things that Euler-Lagrange forms give you, such as making it obvious when a particular coordinate doesn’t actually contribute to the behavior of the system, or letting you look at energy instead of forces, the Hamiltonian also gives you, and the Hamiltonian can be used to do more later on.

What is Physics all about?

Over on the Reading Penrose blog, Jean Louis Van Belle (and I apologize if I’ve got the name capitalized or punctuated wrong but I couldn’t find the author’s name except in a run-together, uncapitalized form) is trying to understand Roger Penrose’s Road to Reality, about the various laws of physics as we understand them. In the entry for the 6th of December, “Ordinary Differential equations (II)”, he gets to the question “What’s Physics All About?” and comes to what I have to agree is the harsh fact: a lot of physics is about solving differential equations.

Some of them are ordinary differential equations, some of them are partial differential equations, but really, a lot of it is differential equations. Some of it is setting up models for differential equations. Here, though, he looks at a number of ordinary differential equations and how they can be classified. The post is a bit cryptic — he intends the blog to be his working notes while he reads a challenging book — but I think it’s still worth recommending as a quick tour through some of the most common, physics-relevant, kinds of ordinary differential equation.

The Intersecting Lines

I haven’t had much chance to sit and think about this, but that’s no reason to keep my readers away from it. Elke Stangl has been pondering a probability problem regarding three intersecting lines on a plane, a spinoff of a physics problem about finding the center of mass of an object by the method of pinning it up from a couple different points and dropping the plumb line. My first impulse, of turning this into a matrix equation, flopped for what were as soon as I worked out a determinant obvious reasons, but that hardly means I’m stuck just yet.

October 2013’s Statistics

It’s been a month since I last looked over precisely how not-staggeringly-popular I am, so it’s time again.
For October 2013 I had 440 views, down from September’s 2013. These came from 220 distinct viewers, down again from the 237 that September gave me. This does mean there was a slender improvement in views per visitor, from 1.97 up to 2.00. Neither of these are records, although given that I had a poor updating record again this month that’s all tolerable.

The most popular articles from the past month are … well, mostly the comics, and the trapezoids come back again. I’ve clearly got to start categorizing the other kinds of polygons. Or else plunge directly into dynamical systems as that’s the other thing people liked. October 2013’s top hits were:

The country sending me the most readers again was the United States (226 of them), with the United Kingdom coming up second (37). Austria popped into third for, I think, the first time (25 views), followed by Denmark (21) and at long last Canada (18). I hope they still like me in Canada.

Sending just the lone reader each were a bunch of countries: Bermuda, Chile, Colombia, Costa Rica, Finland, Guatemala, Hong Kong, Laos, Lebanon, Malta, Mexico, the Netherlands, Oman, Romania, Saudi Arabia, Slovenia, Sweden, Turkey, and Ukraine. Finland and the Netherlands are repeats from last month, and the Netherlands is going on at least three months like this.

Reading the Comics, October 26, 2013

And once again while I wasn’t quite looking we got a round of eight comic strips with mathematical themes to review. Some of them aren’t even about kids not understanding fractions, if you can imagine.

Jason Chatfield’s Ginger Meggs (October 14) does the usual confused-student joke. It’s a little unusual in having the subject be different ways to plot data, though, with line graphs, bar graphs, and scatter graphs being shown off. I think remarkable about this is that line graphs and bar graphs were both — well, if not invented, then at least popularized — by one person, William Playfair, who’s also to be credited for making pie charts a popular tool. Playfair, an engineer and economist of the late 18th and early 19th century, and I do admire him for developing not just one but multiple techniques for making complicated information easier to see.

Eric the Circle (October 16) breaks through my usual reluctance to include it — just having a circle doesn’t seem like it’s enough — because it does a neat bit of mathematical joking, in which a cube looks “my dual” in an octahedron. Duals are one of the ways mathematicians transform one problem into another, that usually turns out to be equivalent; what’s surprising is that often a problem that’s difficult for the original is easy, or at least easier, for the dual.

Continue reading “Reading the Comics, October 26, 2013”

From ElKement: On The Relation Of Jurassic Park and Alien Jelly Flowing Through Hyperspace

I’m frightfully late on following up on this, but ElKement has another entry in the series regarding quantum field theory, this one engagingly titled “On The Relation Of Jurassic Park and Alien Jelly Flowing Through Hyperspace”. The objective is to introduce the concept of phase space, a way of looking at physics problems that marks maybe the biggest thing one really needs to understand if one wants to be not just a physics major (or, for many parts of the field, a mathematics major) and a grad student.

As an undergraduate, it’s easy to get all sorts of problems in which, to pick an example, one models a damped harmonic oscillator. A good example of this is how one models the way a car bounces up and down after it goes over a bump, when the shock absorbers are working. You as a student are given some physical properties — how easily the car bounces, how well the shock absorbers soak up bounces — and how the first bounce went — how far the car bounced upward, how quickly it started going upward — and then work out from that what the motion will be ever after. It’s a bit of calculus and you might do it analytically, working out a complicated formula, or you might do it numerically, letting one of many different computer programs do the work and probably draw a picture showing what happens. That’s shown in class, and then for homework you do a couple problems just like that but with different numbers, and for the exam you get another one yet, and one more might turn up on the final exam.

Continue reading “From ElKement: On The Relation Of Jurassic Park and Alien Jelly Flowing Through Hyperspace”

Reading the Comics, October 8, 2013

As promised, I’ve got a fresh round of mathematics-themed comic strips to discuss, something that’s rather fun to do because it offers such an easy answer to the question of what to write about today. Once you have the subject and a deadline the rest of the writing isn’t so very hard. So here’s some comics with all the humor safely buried in exposition:

Allison Barrows’s PreTeena (September 24, Rerun) brings the characters to “Performance Camp” and a pun on one of the basic tools of trigonometry. The pun’s routine enough, but I’m delighted to see that Barrows threw in a (correct) polynomial expression for the sine of an angle, since that’s the sort of detail that doesn’t really have to be included for the joke to read cleanly but which shows that Barrows made the effort to get it right.

Polynomial expansions — here, a Taylor series — are great tools to have, because, generally, polynomials are nice and well-behaved things. They’re easy to compute, they’re easy to analyze, they’re pretty much easy to do whatever you might want to do. Being able to shift a complicated or realistic function into a polynomial, even a polynomial with infinitely many terms, is often a big step towards making a complicated problem easy.

Continue reading “Reading the Comics, October 8, 2013”

From ElKement: May The Force Field Be With You

I’m derelict in mentioning this but ElKement’s blog, Theory And Practice Of Trying To Combine Just Anything, has published the second part of a non-equation-based description of quantum field theory. This one, titled “May The Force Field Be With You: Primer on Quantum Mechanics and Why We Need Quantum Field Theory”, is about introducing the idea of a field, and a bit of how they can be understood in quantum mechanics terms.

A field, in this context, means some quantity that’s got a defined value for every point in space and time that you’re studying. As ElKement notes, the temperature is probably the most familiar to people. I’d imagine that’s partly because it’s relatively easy to feel the temperature change as one goes about one’s business — after all, gravity is also a field, but almost none of us feel it appreciably change — and because weather maps make the changes of that in space and in time available in attractive pictures.

The thing the field contains can be just about anything. The temperature would be just a plain old number, or as mathematicians would have it a “scalar”. But you can also have fields that describe stuff like the pull of gravity, which is a certain amount of pull and pointing, for us, toward the center of the earth. You can also have fields that describe, for example, how quickly and in what direction the water within a river is flowing. These strengths-and-directions are called “vectors” [1], and a field of vectors offers a lot of interesting mathematics and useful physics. You can also plunge into more exotic mathematical constructs, but you don’t have to. And you don’t need to understand any of this to read ElKement’s more robust introduction to all this.

[1] The independent student newspaper for the New Jersey Institute of Technology is named The Vector, and has as motto “With Magnitude and Direction Since 1924”. I don’t know if other tech schools have newspapers which use a similar joke.

From ElKement: Space Balls, Baywatch, and the Geekiness of Classical Mechanics

Over on Elkement’s blog, Theory and Practice of Trying To Combine Just Anything, is the start of a new series about quantum field theory. Elke Stangl is trying a pretty impressive trick here in trying to describe a pretty advanced field without resorting to the piles of equations that maybe are needed to be precise, but, which also fill the page with piles of equations.

The first entry is about classical mechanics, and contrasting the familiar way that it gets introduced to people —- the whole forceequalsmasstimesacceleration bit — and an alternate description, based on what’s called the Principle of Least Action. This alternate description is as good as the familiar old Newton’s Laws in describing what’s going on, but it also makes a host of powerful new mathematical tools available. So when you get into serious physics work you tend to shift over to that model; and, if you want to start talking Modern Physics, stuff like quantum mechanics, you pretty nearly have to start with that if you want to do anything.

So, since it introduces in clear language a fascinating and important part of physics and mathematics, I’d recommend folks try reading the essay. It’s building up to an explanation of fields, as the modern physicist understands them, too, which is similarly an important topic worth being informed about.

Feynman Online Physics

Likely everybody in the world has already spotted this before, but what the heck: CalTech and the Feynman Lectures Website have put online an edition of volume one of The Feynman Lectures on Physics. This is an HTML 5 edition, so older web browsers might not be able to read it sensibly.

The Feynman Lectures are generally regarded as one of the best expositions of basic physics; they started as part of an introduction to physics class that spiralled out of control and that got nearly all the freshmen who were trying to take it lost. I know the sense of being lost; when I was taking introductory physics I turned to them on the theory they might help me understand what the instructor was going on about. It didn’t help me.

This isn’t because Feynman wasn’t explaining well what was going on. It’s just that he approached things with a much deeper, much broader perspective than were really needed for me to figure out my problems in — oh, I’m not sure, probably something like how long a block needs to slide down a track or something like that. Here’s a fine example, excerpted from Chapter 5-2, “Time”:

Continue reading “Feynman Online Physics”

Gibbs’ Elementary Principles in Statistical Mechanics

I had another discovery from the collection of books at archive.org, now that I thought to look for it: Josiah Willard Gibbs’s Elementary Principles in Statistical Mechanics, originally published in 1902 and reprinted 1960 by Dover, which gives you a taste of Gibbs’s writings by its extended title, Developed With Especial Reference To The Rational Foundation of Thermodynamics. Gibbs was an astounding figure even in a field that seems to draw out astounding figures, and he’s a good candidate for the title of “greatest scientist to come from the United States”.

He lived in walking distance of Yale (where his father and then he taught) nearly his whole life, working nearly isolated but with an astounding talent for organizing the many complex and confused ideas in the study of thermodynamics into a neat, logical science. Some great scientists have the knack for finding important work to do; some great scientists have the knack for finding ways to express work so the masses can understand it. Gibbs … well, perhaps it’s a bit much to say the masses understand it, but the language of modern thermodynamics and of quantum mechanics is very much the language he spoke a century-plus ago.

My understanding is he published almost all his work in the journal Transactions of the Connecticut Philosophical Society, in a show of hometown pride which probably left the editors baffled but, I suppose, happy to print something this fellow was very sure about.

To give some idea why they might have found him baffling, though, consider the first paragraph of Chapter 1, which is accurate and certainly economical:

We shall use Hamilton’s form of the equations of motion for a system of n degrees of freedom, writing $q_1, \cdots q_n$ for the (generalized) coördinates, $\dot{q}_1, \cdots \dot{q}_n$ for the (generalized) velocities, and

$F_1 q_1 + F_2 q_2 + \cdots + F_n q_n$ [1]

for the moment of the forces. We shall call the quantities $F_1, \cdots F_n$ the (generalized) forces, and the quantities $p_1 \cdots p_n$ , defined by the equations

$p_1 = \frac{d\epsilon_p}{d\dot{q}_1}, p_2 = \frac{d\epsilon_p}{d\dot{q}_2}, etc.,$ [2]

where $\epsilon_p$ denotes the kinetic energy of the system, the (generalized) momenta. The kinetic energy is here regarded as a function of the velocities and coördinates. We shall usually regard it as a function of the momenta and coördinates, and on this account we denote it by $\epsilon_p$ . This will not prevent us from occasionally using formulas like [2], where it is sufficiently evident the kinetic energy is regarded as function of the $\dot{q}$ ‘s and $q$ ‘s. But in expressions like $d\epsilon_p/dq_1$ , where the denominator does not determine the question, the kinetic energy is always to be treated in the differentiation as function of the p’s and q’s.

(There’s also a footnote I skipped because I don’t know an elegant way to include it in WordPress.) Your friend the physics major did not understand that on first read any more than you did, although she probably got it after going back and reading it a touch more slowly. And his writing is just like that: 240 pages and I’m not sure I could say any of them could be appreciably tightened.

Also, I note I finally reached 9,000 page views! Thank you; I couldn’t have done it without at least twenty of you, since I’m pretty sure I’ve obsessively clicked on my own pages at minimum 8,979 times.

Reblog: Mixed-Up Views Of Entropy

The blog CarnotCycle, which tries to explain thermodynamics — a noble goal, since thermodynamics is a really big, really important, and criminally unpopularized part of science and mathematics — here starts from an “Unpublished Fragment” by the great Josiah Willard Gibbs to talk about entropy.

Gibbs — a strong candidate for the greatest scientist the United States ever produced, complete with fascinating biographical quirks to make him seem accessibly peculiar — gave to statistical mechanics much of the mathematical form and power that it now has. Gibbs had planned to write something about “On entropy as mixed-up-ness”, which certainly puts in one word what people think of entropy as being. The concept is more powerful and more subtle than that, though, and CarnotCycle talks about some of the subtleties.

carnotcycle

Tucked away at the back of Volume One of The Scientific Papers of J. Willard Gibbs, is a brief chapter headed ‘Unpublished Fragments’. It contains a list of nine subject headings for a supplement that Professor Gibbs was planning to write to his famous paper “On the Equilibrium of Heterogeneous Substances”. Sadly, he completed his notes for only two subjects before his death in April 1903, so we will never know what he had in mind to write about the sixth subject in the list: On entropy as mixed-up-ness.

View original post 686 more words

Fun With General Physics

I’m sure to let my interest in the Internet Archive version of Landau, Akhiezer, and Lifshiz General Physics wane soon enough. But for now I’m still digging around and finding stuff that delights me. For example, here, from the end of section 58 (Solids and Liquids):

As the temperature decreases, the specific heat of a solid also decreases and tends to zero at absolute zero. This is a consequence of a remarkable general theorem (called Nernst’s theorem), according to which, at sufficiently low temperatures, any quantity representing a property of a solid or liquid becomes independent of temperature. In particular, as absolute zero is approached, the energy and enthalpy of a body no longer depend on the temperature; the specific heats c_p and c_V, which are the derivatives of these quantities with respect to temperature, therefore tend to zero.

It also follows from Nernst’s theorem that, as $T \rightarrow 0$ , the coefficient of thermal expansion tends to zero, since the volume of the body ceases to depend on the temperature.

General Physics from the Internet Archive

Mir Books is this company that puts out downloadable, translated copies of mostly Soviet mathematics and physics books. As often happens I started reading them kind of on a whim and kept following in the faith that someday I’d see a math text I just absolutely had to have. It hasn’t quite reached that, although a post from today identified one I do like which, naturally enough, they aren’t publishing. It’s from the Internet Archive instead.

The book is General Physics, by L D Landau, A I Akhiezer, and E M Lifshiz. The title is just right; it gets you from mechanics to fields to crystals to thermodynamics to chemistry to fluid dynamics in about 370 pages. The scope and size probably tell you this isn’t something for the mass audience; the book’s appropriate for an upper-level undergraduate or a grad student, or someone who needs a reference for a lot of physics.

So I can’t recommend this for normal readers, but if you’re the sort of person who sees beauty in a quote like:

Putting r here equal to the Earth’s radius R, we find a relation between the densities of the atmosphere at the Earth’s surface (n_E) and at infinity (n_∞):

$n_{\infty} = n_E e^{-\frac{GMm}{kTR}}$

then by all means read on.

Reblog: Random matrix theory and the Coulomb gas

inordinatum’s guest blog post here discusses something which, I must confess, isn’t going to be accessible to most of my readers. But it’s interesting to me, since it addresses many topics that are either directly in or close to my mathematical research interests.

The random matrix theory discussed here is the study of what we can say about matrices when we aren’t told the numbers in the matrix, but are told the distribution of the numbers — how likely any cell within the matrix is to be within any particular range. From that start it might sound like almost nothing could be said; after all, couldn’t anything go? But in exactly the same way that we’re able to speak very precisely about random events in the context of probability and statistics — for example, that a (fair) coin flipped a million times will come up tails pretty near 500,000 times, and will not come up tails 600,000 times — we’re able to speak confidently about the properties of these random matrices.

In any event, please do not worry about understanding the whole post. I found it fascinating and that’s why I’ve reblogged it here.

inordinatum

Today I have the pleasure of presenting you a guest post by Ricardo, a good physicist friend of mine in Paris, who is working on random matrix theory. Enjoy!

After writing a nice piece of hardcore physics to my science blog (in Portuguese, I am sorry), Alex asked me to come by and repay the favor. I am happy to write a few lines about the basis of my research in random matrices, and one of the first nice surprises we have while learning the subject.

In this post, I intent to present you some few neat tricks I learned while tinkering with Random Matrix Theory (RMT). It is a pretty vast subject, whose ramifications extend to nuclear physics, information theory, particle physics and, surely, mathematics as a whole. One of the main questions on this subject is: given a matrix $latex M$ whose entries are taken randomly from a…

View original post 1,082 more words

Reblog: Making Your Balls Bounce

Neil Brown’s “The Sinepost” blog here talks about an application of mathematics I’ve long found interesting but never really studied, that of how to simulate physics for game purposes. This particular entry is about the collision of balls, as in for a billiard ball simulation.

It’s an interesting read and I do want to be sure I don’t lose it.

The Sinepost

In this post, we will finally complete our pool game. We’ve already seen how to detect collisions between balls: we just need to check if two circles are overlapping. We’ve also seen how to resolve a collision when bouncing a ball off a wall (i.e. one moving object and one stationary). The final piece of the puzzle is just to put it all together in the case of two moving balls.

Bouncy Balls

The principle behind collision resolution for pool balls is as follows. You have a situation where two balls are colliding, and you know their velocities (step 1 in the diagram below). You separate out each ball’s velocity (the solid blue and green arrows in step 1, below) into two perpendicular components: the component heading towards the other ball (the dotted blue and green arrows in step 2) and the component that is perpendicular to the other…

View original post 303 more words

The Box Drops

So the last piece I need for figuring out whether it’s easier to tip a box over by pushing on the middle of an edge or along one corner is to know the amount of torque applied by pushing with, presumably, the same force in both locations. Well, that’s almost the last bit. I also need to know how the torque and the moment of inertia connect together to say how fast an angular acceleration I can give the box.

Continue reading “The Box Drops”

A Third Thought About Falling

I’m surprised my father let me get away with it. I assume that he was just being courteous and letting me get to my next points in studying whether a box is easier to tip over by pushing from the center of one of its edges or by pushing from its corner. Or he’s figured it’s too much bother to write a response; he’s been living his computer life on an iPod for a long while now and I can’t figure how he types at any length on that.

Continue reading “A Third Thought About Falling”

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

How fast would the Earth have to spin in order to cause weightlessness at the…

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Kindly share this:

Bouncy Balls

Kindly share this:

Kindly share this:

Kindly share this: